이전에도 말했듯이 행렬과 벡터는 뗄레야 뗄 수 없는 사이가 되었다.
그렇지만 우리는 그 사이를 모르기에
조심스럽게 행렬과 벡터에게 말을 걸어야 한다.
걸어보자
사실 이전 글에서
행렬의 종류를 배울 때
왜 열 벡터?, 행 벡터? 왜 행렬을 벡터라고 했는지 궁금했을 수도 있다.
솔직히 안 궁금했어도 알아보자
++열 벡터, column-major vector 행 벡터, row-major vector
일반적으로 3차원 공간에서 벡터가 있다고 하면
1 by 3 matrix나 3x1 행렬로 나타낸다.
**보통 수학에서는 열 벡터를 기준으로 삼는다.
우리는 수학을 거스르고 싶지 않기에 나도 열 벡터를 기준으로 삼아서 설명하려고 한다.
일단 벡터를 행렬로 표현할 수 있다면?
벡터 간의 연산도 행렬로 표현할 수 있어야 의미가 있다.
벡터의 기본연산인
합, 스칼라곱은 아래와 같이 나타낸다.

내적의 경우와 외적의 경우는 어떨까?
우선 내적
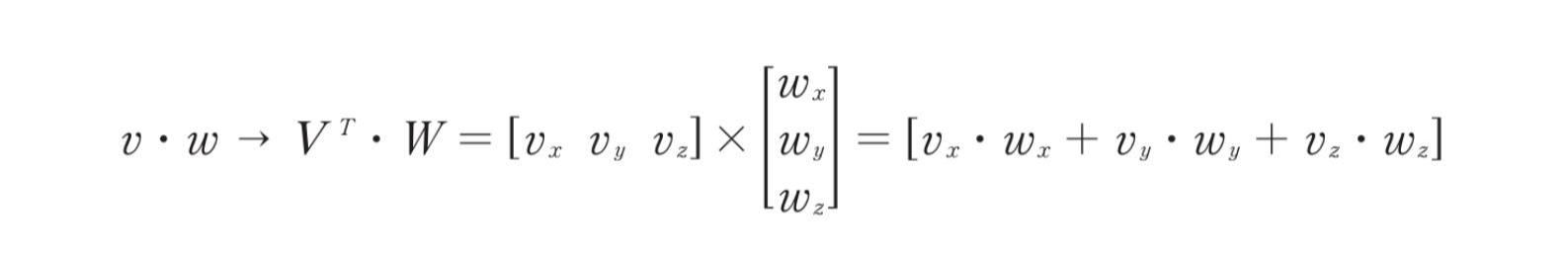
그 다음 외적
++ 기저 벡터는 i, j, k
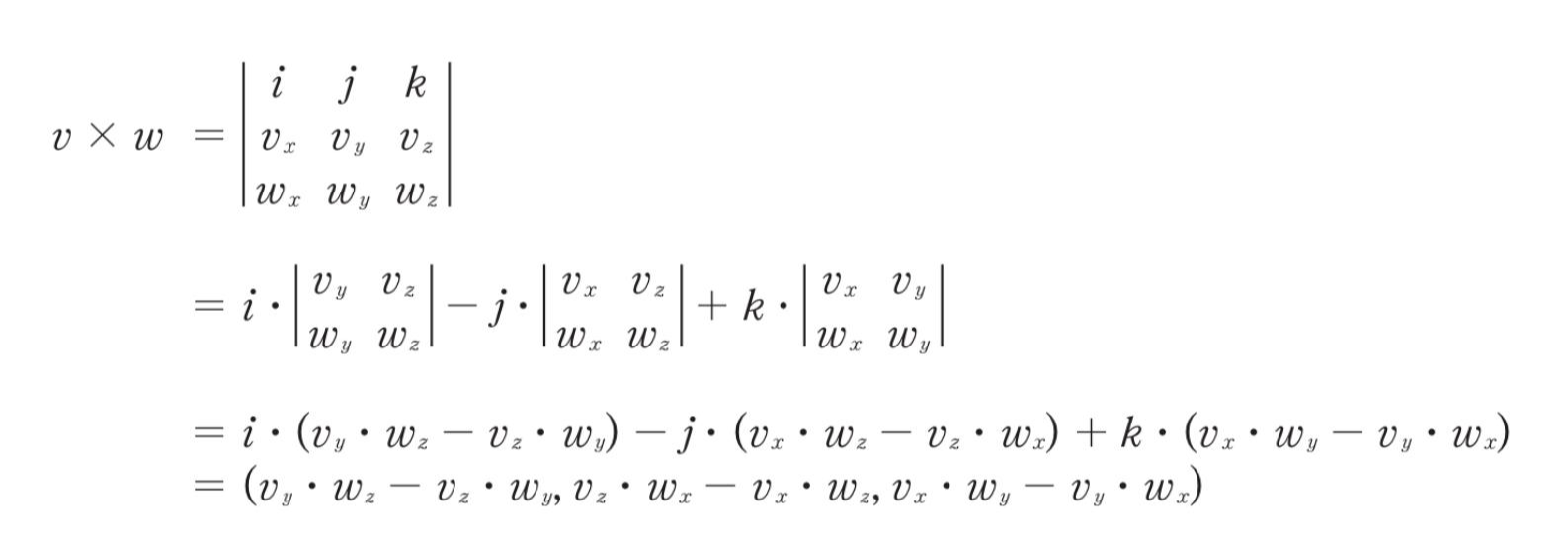
보니깐 행렬로 연산하는 것도 나쁘지 않아 보인다.
흠... 근데 외적 약간 복잡한 것 같은데? 이렇게 쓸 거면 안 쓰는게 낫지 않나?
그래서 만든 것이 행렬 곱연산을 통해서 나타내는 방법이 있다.
솔직히 생긴 게 좋아야 연산도 하고 싶을 거 아닌가?

음.. 보니까 아닌 것 같기도?
V 와 W 곱을 계산하기 위해선
행렬곱으로 외적을 나타내려면 일단 벡터를 이용해서 반대칭 행렬, skew-symmetric matrix를 만들어야 한다.
위와 같은 행렬이 반대칭 행렬이다.
**여기선 V를 기준으로 만든다.
**반대칭 행렬이란 주 대각선을 기준으로 나머지 성분들이 대칭은 되지만 기호는 반대인 행렬을 말한다.
뒤의 벡터는 열 벡터로 만든 후 행렬 곱을 하면 된다.
**뒤의 벡터는 여기서 W를 말한다.

음.. 보기 편하긴 하네
다음으로는 정사영이라고 투영하는 것을 배웠다.
즉, 벡터와 벡터 간의 투영을 하는 것에도 우리는 행렬을 쓸 수 있다.
v를 w에 투영시킨다고 해보자

음..?
그렇다... 이거 간단하잖아?? 그게 뭐??
저 모양을 잘 기억해두고 이 식을 보자.
*** a,b,c는 벡터이고 A,B,C는 행렬이다.
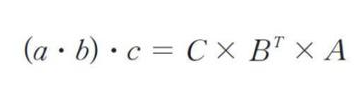
앞에서 내적을 어떻게 표현했더라??
아래와 같이 표현했다.

왜 저렇게 되는지?는 확인해보면 된다.
그렇게 중요하지는 않다.
하지만 우리는
C와 B(T)를 곱하는 연산을 tensor product, 텐서곱이라 부른다. 새로운 기호도 써서 나타낸다.
그래서 텐서곱으로 바꿔서 표현하면 아래와 같다.

그렇다면 투영하는 벡터를 구하는 공식을 이렇게 바꿀 수도 있다.

와!!
신기하다
마지막으로 스칼라 삼중곱과 행렬식에 대해 알아보려고 한다.
이미 다 알아봤지만

다시 다르게 알아보자.
행렬로 구성해본 식을 알아보자

역시나 행렬로 표현을 해도 결과는 변함이 없다.
스칼라 삼중곱은 평행육면체의 부피라고 했다.
즉, 세 벡터로 이루어진 행렬의 행렬식의 절대값은 그 벡터들로 이루어진 육면체의 부피가 된다는 뜻이다.
2차원에서는...?
행렬식의 값이 그 벡터로 이루어진 평행사변형의 넓이가 되겠다.
벡터와 행렬이 서로 표현될 수 있다는 것을
굳이 몸소 느껴 보았다.
나쁘지 않았다.
'Game Development, 게임개발 > 게임 수학,물리' 카테고리의 다른 글
| 선형 변환- 크기변환(Scaling), 회전변환(Rotation) [게임수학] (0) | 2021.03.18 |
|---|---|
| 선형변환, Linear Transformation [게임수학] (0) | 2021.03.17 |
| 행렬, Matrix - 2, 가우스 요르단 소거법, 역행렬, 행렬식, Determinant [게임수학] (0) | 2021.03.12 |
| 행렬, Matrix - 1, 연립1차방정식, 가우스 소거법 [게임수학] (0) | 2021.03.11 |
| 벡터(Vector) - 3(외적, Cross product) [게임수학] (0) | 2021.03.10 |