어떠한 값을 찾을 때
정렬이 되어있는 데이터들 안에서(이게 핵심이다)
정렬하는데 시간이 더 걸린다면 그냥 이진탐색 사용하지 않는게 낫다.
선형 탐색보다 훨씬 빠른 탐색속도를 가진 이진탐색이다.
일반적으로 Array가 이용된다.
우선보자
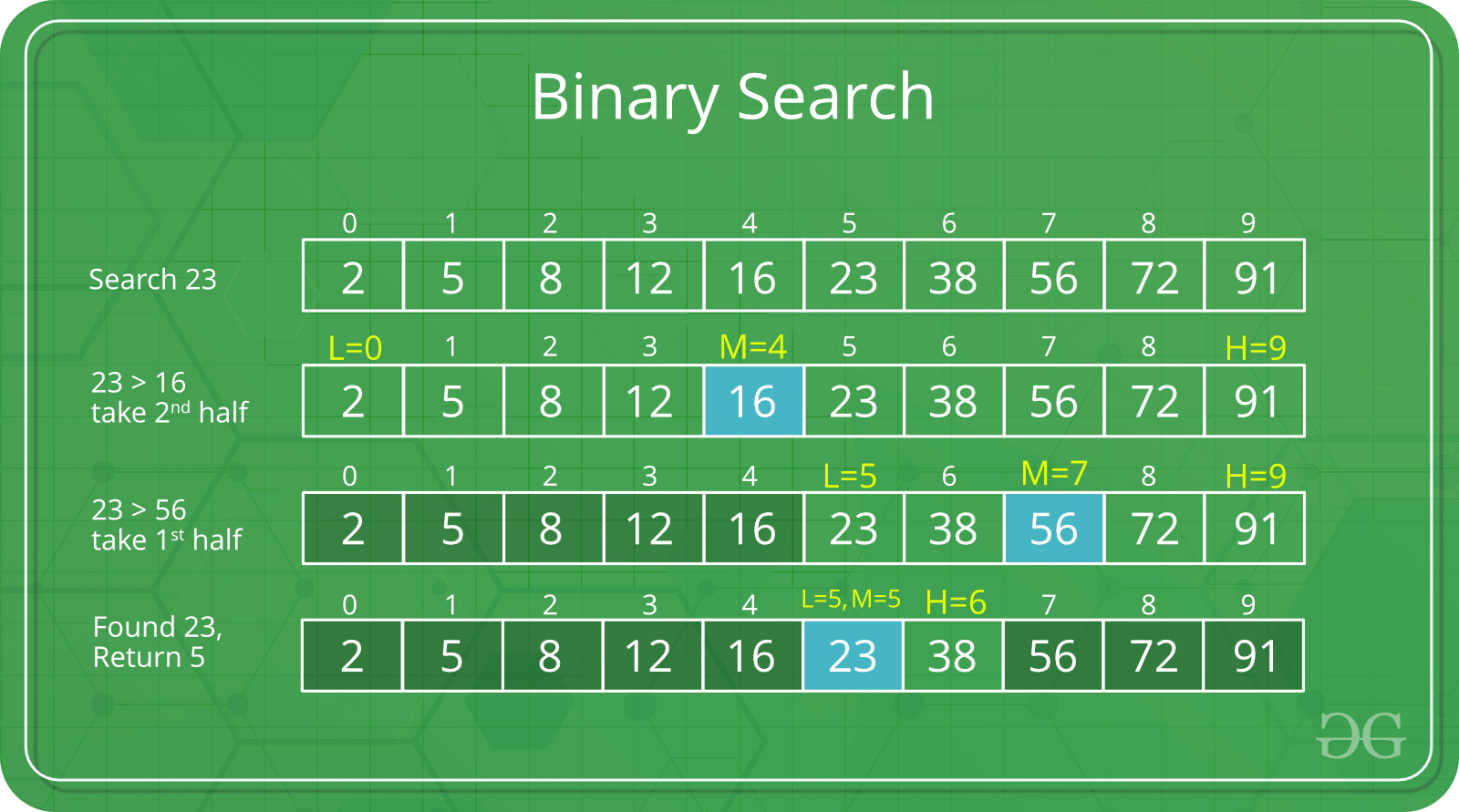
23을 찾기 위해서
중앙값을 조사한다.
중앙값보다 크기에
이번에는 중앙값으로 나눠진 오른쪽 그룹에 대해 중앙값을 조사한다.
그 나눠진 그룹의 중앙값보다는 작기에
다시 왼쪽 그룹을 만들어 조사한다.
나올 때까지 조사한다.
만약 값이 없다면
값이 없는 것은 어떻게 판단할 수 있을까??
다시 보자
이번엔 24를 찾는다고 해보자

0-9까지 10개의 원소가 있다.
4번 인덱스를 조사했고 해당 값이 더 커서
5번부터 9번까지 사이의 중앙값인 7번을 조사했다.
7번보다는 작아서
5번과 6번 인덱스의 중앙값인 5를 조사했다.
그러나 24는 23보다 크기에 오른쪽 그룹을 조사하려고 한다.
그러나 Low가 6번 인덱스가 되고 High가 6번 인덱스가 되는 상황이 발생한다.
같아지는 것이다.
같아지면 그 값이 해당 값이 아니라면 Low와 High가 그 다음에는 조사할 남은 원소가 없기때문에 종료되어야 한다.
그 때 인덱스가 역전이 된다.
Low가 High보다 커지는 상황이 온다.
이때 찾으려는 값이 없다고 판단할 수 있다.
즉, Low > High일 때 이진탐색은 종료된다.
이렇게 표현하는 사람도 있다.
High - Low < 0
뭐 같은 표현인데 역전을 표현하려면
Low > High
이게 더 잘표현하지 싶다.
이 이진탐색은 항상 남은 원소의 절반씩을 날리기 때문에
O(log N)의 시간복잡도를 가진다.
구현은 어떻게 하는가?
반복문과 재귀문이 있다.
int binarySearch(int arr[], int target) {
int low = 0; // 가장 왼쪽 인덱스
int high = arr.length - 1; // 가장 오른쪽 인덱스
int mid;
while(low <= high) {
mid = (low + high) / 2; // 중앙값(int이므로 알아서 정수가됨)
if (arr[mid] == target) // 중앙값이 찾는 값이면 바로 반환
return mid;
else if (arr[mid] > target) // 왼쪽그룹 조사 + mid는 해당값이 아니니 mid-1부터 조사
high = mid - 1;
else
low = mid + 1; // 오른쪽 그룹 조사 + mid는 해당값이 아니니 mid + 1부터 조사
}
return 0;
}
재귀
int BSearchRecursive(int arr[], int target, int low, int high) {
if (low > high) // 재귀 base condition
return -1;
int mid = (low + high) / 2;
if (arr[mid] == target) // 찾았으면 값 반환하고 종료
return mid;
else if (arr[mid] > target) // 못찾았으면 해당 그룹에서 다시 함수실행
return BSearchRecursive(arr, target, low, mid-1);
else // 못찾았으면 해당 그룹에서 다시 함수실행
return BSearchRecursive(arr, target, mid+1, high);
}
참고로 배열이 아니라 iterator로 만든다면..?
bool binary_search(int target, std::vector<int>& S)
{
auto first = S.begin();
auto last = S.end();
while(true)
{
//현재 검색 범위의 중간 원소를 저장함
auto range_length = std::distance(first, last); //first부터 end까지의 길이
auto mid_element_index = first + std::floor(range_length/2); //first 부터 중간위치에 있는 iterator
auto mid_element = *(first + mid_element_index); //해당 위치에 있는 원소 값
if(mid_element == N ) return true; //찾음
//중간값이 오른쪽에 있으면 왼쪽 그룹을 조사
else if(mid_element > N) {
std::advance(last, -mid_element_index);
//last = mid_element_index - 1; -> 위와 동치
}
//중간값이 왼쪽에 있으면 오른쪽 그룹을 조사
else if(mid_element < N){
std::advance(first, mid_element_index);
//first = mid_element_index + 1; -> 위와 동치
}
//만약 현재 범위(range_length) 가 1이면 false;
if(range_length == 1) return false; //다시 말해서 first와 last 차이가 1이면
//-> end는 마지막 원소가 아닌 마지막 원소의 1칸 뒤를 반환한다.
}
}
'문제풀이(Problem Solving) > C++ 문제풀이에 유용한 것들' 카테고리의 다른 글
| Graph, 그래프 , 자료구조 [CPP] (0) | 2021.07.05 |
|---|---|
| C++ 코딩테스트에 유용한 것들 [CPP] (0) | 2021.06.18 |
| STL 우선순위 큐, Priority Queue 사용법 [C++] (0) | 2021.06.13 |
| STL 셋, 집합, set 사용법 [C++] (0) | 2021.06.13 |
| STL 맵, map 사용법 [C++] (0) | 2021.06.12 |