3D 게임에서는
플레이어의 몰입을 위해 물체들을 실사와 같게 만드려고 노력한다.
그 중 빛에 대해서 실제와 같이 표현하려고 한다.
빛은 게임 속에서 어떻게 구현할 수 있을까???
우리는 광원이 있다면
해당 광원에 대해서 물체의 어느 부분의 밝기를 올려야 하는가?
라는 질문을 하게 된다.

구가 있다고 해보자.
광원이 어디있다고 생각하는가?
아마 바로 머리위에서 조금 왼쪽에 있다고 생각할 것이다.
왜 이 그림을 보자마자 그렇게 느꼈나?
저것도 실제가 아닌 그림일 뿐인데..?
그 이유는 정말 실제와 같이 생겼기 때문이다.
구의 좌표를 알고 광원에 대한 방향벡터를 알 수 있다면 해당 지점에서의 밝기를 결정할 수 있겠다.
우선 정사영이란 것을 배웠다면 이해하기는 쉬워진다.

정사영은 직선으로 빛이 내리쬐고 물체에는 빛이 닿는 부분과 빛이 닿지 않는 부분이 있다.
구의 원점에서 구의 한 좌표를 가리키는 방향벡터를 생각해보자.
해당 벡터는 구에 수직인 벡터이다. (고등수학)
즉, 해당 벡터가 곧 그 좌표와 접하는 평면의 법선벡터가 된다는 말과 같다.
다시 말해 해당 좌표에 대한 벡터와 광원의 방향벡터를 비교하여
해당 좌표가 광원과 이루는 각이 얼마인지 계산이 가능하다.
이렇게 생각해보자
1. 면에 수직인 벡터(이하 법선벡터)가 광원과 이루는 각이 180도라면 밝기 최대
2. 법선벡터가 광원 방향벡터와 이루는 각이 90도면 최소
3. 면의 법선벡터가 90보다 작아지면 밝기는 최소( 광원의 반대편은 빛이 닿지 않음)
이렇게 말했지만 법선벡터를 원의 중심으로 잡냐 원의 바깥으로 잡냐의 차이다.
우선 저런 식으로 구현하겠구나 생각하면 된다.
하지만 빛의 밝기가 정말 각도에 정비례하게 감소할까?가 문제다.
실제로 위의 구를 보면 뭔가 3차함수의 곡선느낌이 나는듯 하다.
결국 해당 밝기의 감소형태는
구의 질감이 결정한다.
빛의 반사를 많이 하는 물체가 있는 반면 빛을 흡수하는 물체도 있을테니까..?
하지만 밝기의 변화를 물체에 따라 다르다고만 해버리면
컴퓨터는 값이 주어지지 않은 값에 대해서는 계산할 수가 없다.
그래서 우리는 위대한 모델을 끌고 온다.
전형적으로 물체의 밝기 곡선을 사용해서 렌더링하는 것이다.
람베르트 반사 모델이다. , Lambert라고 한다.
우리는 공학자이다. 어떻게 저런 것을 유도했지? 는 쓰지 않는다.
증명해줬으면 알차게 써주면 된다.
위키백과에서는 아래와 같이 말한다.
램버시안 반사율(Lambertian reflectance)을 갖는 표면은, 관찰자가 바라보는 각도와 관계없이 같은 겉보기 밝기를 갖는다.
즉, 예를 들어 표면처리를 하지 않은 원목 재질은 보는 각도에 따라 밝기가 다르게 보이지 않으므로 거의 램버시안 반사율을 갖는다.
그러나 폴리우레탄으로 반짝이는 처리를 한 목재는 광원의 위치에 따라 거울면과 같은 하이라이트를 가질 수 있다.
다시 말하면 다 램버시안 반사율을 가지는 것은 아니지만
표면에 대해서 정보가 없어서 람베르트 반사율을 적용한다면 적절한 근사치가 되는 경우가 많다는 말이다.
식으로는 이렇게 표현한다.
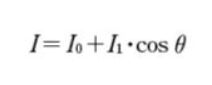
I : 색의 밝기
I0 : 환경광(Ambient Light)의 밝기
I1 : 직사광(Directional Light)의 밝기
theta : 광원 방향과 면의 법선벡터가 이루는 각
** 환경광이란 광원의 각도와 관계없이 일정한 밝기로 면을 비추는 빛으로 모든 방향에서 일정한 밝기로 오는 빛을 의미한다.
이 밝기가 전체 밝기에 영향을 주는 이유는
주변의 다른 물체에서 반사된 빛이 비치는 효과를 주기 위해서다.
하지만 밝기를 계산하려는 면에서 가까운 밝은색 물체가 있다면
해당 물체가 반사하는 빛때문에 해당 면 또한 더욱 밝게 표현되어야 한다.
그렇게 되면 하나의 물체를 렌더링할 때마다 다른 물체의 반사광에 대해서 계산을 해야한다.
이는 현실적으로 불가능(할 수 있지만 효과에 비해서 계산량이 무지 많아져서 비효율)이다.
++저사양에서도 게임이 돌아가게 하려면 효율적으로 만들어야 한다.
그래서 실제로 3D 게임에서는 실시간 렌더링이더라도 환경광을 근사해서 사용한다.
그렇다면 람베르트 반사식을 어떻게 쓸까??
환경광은 그냥 구한다고 치고..
직사광에 코사인값?
음.. 코사인 값이 들어간 공식을 어디서 배웠더라??
는 내적이다.
즉, 법선벡터와 광원의 방향벡터를 내적해보자.하지만 각도를 아는 것이 아니기 때문에
내적을 구하는 다른 방법인 성분 곱의 합으로 구하면된다.

성분 곱의 합은?

a,b의 크기는 제곱의 합을 루트 씌우면 되겠지?
법선벡터를 n, 방향벡터를 l이라고 한다면
람베르트 반사식은 이렇게 바뀔 수 있다.

그리고 직사광에 대해서는 고정되어있기 때문에
항상 l 값은 고정되어있고
n(법선벡터)만 좌표에 따라 새로 구해서 계산해주면 해당 위치의 밝기 값을 알 수 있겠다.
앞서 말했듯이 표면의 특징을 모를 때는 그냥 근사치를 가져다 쓴다고 했다.
즉, 람베르트 반사식을 이용하면 표면의 특징을 바꿀 수 있다는 말로 들린다.
그것이 맞다.

즉, 해당 식에서 직사광의 주는 영향을 바꿔야 한다는 의미다.
저기 I1과 내적되는 저 광원 방향벡터와 법선벡터의 내적 값을 바꾸는 것이다.
저 해당되는 부분을 거듭제곱을 함으로써 바꿀 수 있다.
어차피 해당 벡터에 대해서는 단위벡터이기 때문에
거듭제곱을 한다고해서 밝기 자체가 원래의 값보다 커질 수 없다.
거듭제곱을 함으로써 얻는 질감은
제곱한 것의 질감이 더 매끄럽고 반질반질해진다는 느낌을 주게 된다.
'Game Development, 게임개발 > 게임 수학,물리' 카테고리의 다른 글
| 게임수학 - 동차좌표계, Homogeneous coordinates ** (4) | 2021.09.05 |
|---|---|
| 게임물리 - 회전 (0) | 2021.09.03 |
| 게임 물리 - 안티앨리어싱, AA ( Anti-Aliasing) (0) | 2021.09.02 |
| 게임 물리 - 충돌 판정 (0) | 2021.08.27 |
| 게임 물리 - 원근감의 표현 (0) | 2021.08.22 |