저번에 이진트리에서 삽입, 연산, 탐색에 대해 함수를 만들고 넘어가지 않았다.
왜냐하면 선형적인 구조의 자료구조가 아니기 때문에
연산 후에도 이러한 계층적 자료구조의 형태를 유지하기 위해
따로 해줘야 하는 부분이 있어서 그랬다.
즉, 트리의 조건을 유지하면서 연산을 수행해야한다.
그 연산을 하기 위해서 BST라는 것을 이용해보자
우선 이진탐색트리를 정의하자면
1. key(왼쪽서브트리)≤key(루트노드)≤key(오른쪽서브트리)
2. 이진탐색를 중위순회하면 오름차순으로 정렬된 값을 얻을 수 있다.

그렇다면 이 이진트리는 정렬된 것일까?
맞다.
거의 모든 데이터들은 정렬되었을 때 의미를 가지게 된다.
탐색연산
이진탐색트리에서 특정한 값을 찾는다. 그렇다면 무엇을 기준으로 찾을까?
바로 key 값입니다. 트리기 때문에 root, 즉, 중간값부터 시작한다.

이렇게 12를 찾는데 루트보다 key 값이 작으니까 왼쪽 자식으로
그다음에는 크므로 오른쪽 자식으로 이렇게 왔다갔다 하면서 키 값을 탐색한다.

이런식으로 순환을 통해서 만드는 것이 정말 좋다. 우선 트리에서는 재귀로 만드는 것이 훨씬 낫다.

반복문으로도 할 수 있지만 뭐... 재귀가 더 간단하다.
탐색은 key 값을 찾을 때 까지하고 결국 단말노드까지가서도 못찾으면 NULL을 반환한다.
삽입연산
원래 다들 삽입연산부터 알아보는데 왜 탐색부터 알아봤을까?
삽입하려면 탐색을 해야하기 때문이다.
선형적이 아니라 맨 뒤, 맨 앞에 바로 접근이 안된다.
삽입하려는 값을 정하고 그 값을 탐색해서 없으면? 그 때 도착한 단말노드에 노드를 삽입한다.

구현은 이렇게 한다.

우선 함수에서 n이 새로만드려는 노드의 포인터다. r이 부모노드를 가리키는 포인터다.
첫번째 줄에서 중복여부를 검사한다.
-> 바로 종료
결국 중복되지 않는 선에서 삽입할 수 있는 위치까지 간다.
그래서 NULL일 때는 n이 되지만 NULL이 아니면 함수를 다시 한번 선언한다.
왜냐면 null 이아니면 삽입할 수 없으니까.
삭제연산
근데 삭제는 조금 어렵다. 왜냐면 삽입은 갈 때 까지 가서 삽입을 했지만
삭제는 아무곳에서나 가능하게 만들어야한다.
그래서 3가지 케이스가 있다.
1. 단말노드를 삭제하는 경우
2. 자식이 1개라도 있는 경우
3. 자식이 2개있는 경우
우선 1번
단말노드의 부모노드를 찾아가서 자식과 연결을 끊으면 된다.

2번의 경우
노드를 삭제하고 자식을 할아버지랑 이어준다.

3번 경우가 가장 복잡하다.
부모노드가 없어졌으니 할아버지노드랑 이어져야하는데 어떤 자식놈을 이어야할지 정해야하기 때문이다.
처음에 말했다시피 자식놈이 이렇게 올라가더라도 이진탐색트리의 성질을 깨면 안된다.
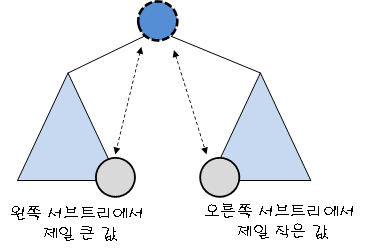
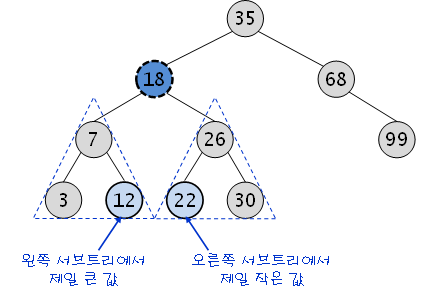
그래서 왼쪽서브트리의 가장 우측 자식, 오른쪽서브트리의 가장 왼쪽 자식을 비교해서 올린다.
구현은 아래와 같이 한다.

'컴퓨터(Computer Science) > 자료구조(Data Structure)' 카테고리의 다른 글
| [C언어] 자료구조 - 우선순위 큐 heap 힙 -2 (0) | 2019.12.18 |
|---|---|
| [C언어] 자료구조 - 우선순위 큐 priority queue -1 (0) | 2019.12.18 |
| [C언어] 자료구조 - Tree 트리 순회,기본연산 -3 (0) | 2019.12.15 |
| [C언어] 자료구조 - Tree 트리 구현 -2 (0) | 2019.12.15 |
| [C언어] 자료구조 - Tree 트리 -1 (0) | 2019.12.15 |