벡터를 이어서 공부할 건데
내적을 공부해 볼 생각이다.
하지만 주제가 게임 수학이니만큼... 어디에다 쓰일 수 있을지 생각해보면서 배워보자
단순히 벡터 내적이 무슨 뜻인지 부터 알아보자
영어로는, Dot Product, Inner Product라고 한다.
보통 내적은 벡터의 방향이 얼마나 일치하는 지의 용도로 쓰인다. -> 벡터 간의 유사도로 쓰이는 경향이 있음
그래서 내가.. NLP할 때 유사도를 많이 사용했지 ㅎ

만약 해당되는 2개의 벡터가 크기가 1이라면 벡터 사이각에 대한 cos 값을 얻을 수도 있다.
또한 벡터의 성분으로도 내적을 구할 수 있다.
**또한 자기 자신과 내적을 할 경우에는 자신의 크기 제곱을 구할 수 있다.
-> 실제 프로그래밍에서는 벡터의 길이보다 길이의 제곱을 사용하는 경우가 더 많다.
이유는 제곱근을 구하는 것이 느려서 그렇다.
실제로 Unity 에서는 벡터 내적 계산을 이렇게 한다.
Vector3.Dot(VectorA, VectorB)
내적을 잘 살펴보면 cos 값이 들어간다. 즉, 벡터 간의 사이각에 따라 값이 완전히 바뀔 수 있다.
즉, 내적을 통해서 두 벡터의 방향 관계를 알 수 있다는 것이다.
이것이 왜 중요하냐?
예를 들면 적과 플레이어의 위치관계를 내적을 통해 알 수 있다.
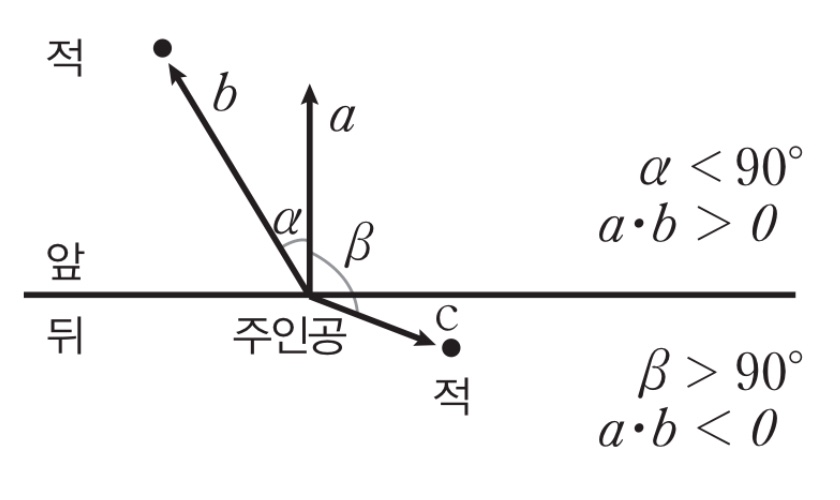
플레이어의 방향벡터와 적으로의 방향벡터의 내적 값이 음이면 플레이어 뒤에 존재하는 것이고
양이면 앞에 존재하는 것이다.
아래 그림을 통해 이해해보자
만약 두 벡터가 크기가 1인 단위 벡터가 된다면 다른 정보도 얻을 수 있다. ( 하지만 실제 코드로는 부동 소수점 표현의 특성 상 두 값을 단순히 비교해서 결정하기는 어렵다)
두 벡터가 평행인지 아닌지 알 수 있는 것이다.
-> 그렇다고 해서 평행을 알기 위해서 단위 벡터가 아닌 벡터들을 정규화할 필요는 없다.
정규화는 연산을 더 필요로 하기 때문에 외적을 이용해 평행임을 알아내는 것이 더 효율적이다.
평행이라면 사이각이, 라디안 값이 0, pi가 되어야 하므로 값이 1이거나 -1 여야한다.
또한 내적은 어떤 벡터를 중심으로 정해진 각 범위 내에 물체가 존재하는지 판별하는 데도 유용하다.
** 범위 공격, 범위 기반 스킬들에 유용할 것같다.
예를 들어서 적에게 시야각이 있고 플레이어가 잠입 시에 들켰는지를 확인해보는 매커니즘을 설계하고자 한다.
적의 현재 방향 벡터를 v, 적이 플레이어에게 향하는 벡터를 w, 적의 시야각을 a라고 해보자.

즉, v,w의 사이각을 b라고 하면 이것이 a/2보다 작아지면 들켰다라고 생각할 수 있다.

++ LOL의 카시오페아 궁을 아는가?
카시오페아 궁의 메커니즘을 생각해보면
카시오페아와 마주하고 있으면 궁극기에 걸려 마비가 된다.

유명한 짤이다.
페이커의 궁극기 피하기
라이엇이 각 플레이어의 시야각을 얼마나 해놓았는지, 궁의 범위는 얼마인지는 정확히 모르지만
매커니즘을 생각해보자면
마주보고 있으면 무조건 궁극기에 걸린다. 즉. 서로의 방향벡터가 이루는 각 + 시야각에 따라 걸릴 것이다.
대충 따져보자면
내적해봤을 때 음수이면서, 궁의 범위 안에 있고 방향벡터와 시야각과 사이의 각도에 따라 뭐 걸리게해놨지 않았을까?
개인적인 생각이다.
또 뭐가 있을까?
정사영이라고 들어봤나..? 중,고등학교를 잘 공부했으면 알 수도 모를 수도 ㅎ
아무튼 어떤 벡터를 다른 벡터에 투영할 때 내적을 이용한다.
++ 투영을 projection이라고 한다. (빔 프로젝트하는 것처럼 무엇인가 쏠 때 그것을 project라고 한다)
?? 투영할 일이 뭐가 있는데요??
예를 들어서 어떤 벡터를 새로운 좌표계에 옮길 때 유용하다.
라떼는 일차변환이라고 해서.. 맨날 좌표계 옮겼는데.. 아무튼 그렇다 ㅋㅋㅋㅋ
또한 충돌 검사에서 한 벡터를 다른 벡터에 투영하는 경우도 있다.
내적은 이정도로 하고
외적을 다음에 공부해보자
'Game Development, 게임개발 > 게임 수학,물리' 카테고리의 다른 글
| 행렬, Matrix - 1, 연립1차방정식, 가우스 소거법 [게임수학] (0) | 2021.03.11 |
|---|---|
| 벡터(Vector) - 3(외적, Cross product) [게임수학] (0) | 2021.03.10 |
| 게임 수학에 관한 참고책[게임수학] (0) | 2021.03.09 |
| 벡터(Vector) - 1 [게임수학] (0) | 2021.03.09 |
| 선형 대수, Linear Algebra [게임수학] (0) | 2021.03.09 |