현실의 운동과 컴퓨터가 계산한 운동이 정확히 같을까?
디지털이 아날로그와 정확히 같을까?
아날로그는 모든 것을 표현할 수 있지만
디지털에는 표현할 수 없는 것이 있다고 흔히 말한다.
아날로그 시계는 이 세상에 존재하는 모든 '시각'을 가리킬 수 있다.
예를 들어 해시계는 연속적이다.
반면 디지털시계는?? 아무리 정확한 시계라도 불연속이다.
서론이 길었다.
즉, 우리는 물체의 운동을 컴퓨터에 구현하는데.. 힘이 많이 든다.
문과로 넘어가게 된 계기들 중 하나인 뉴턴의 첫번째 방정식을 가져와보자
F = ma
Equation of motion이다.
운동방정식인데 이것 때문에 여럿 보냈다.
즉, a = F/m으로 다시 표현될 수 있다.
우리는 위치 - > 속도 - > 가속도를 구할 수 있다.
바로 시간에 대해 미분하면 된다.
즉, 다시 말하면
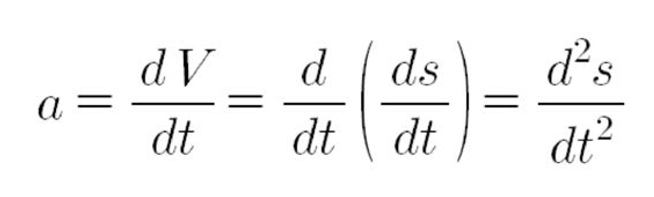
이렇게 된다.
미분이 포함된 식이라
미분 방정식이라고 한다.
대학교에서 공학수학에서 배우는 것들이 이거다.
아무튼
이 미분방정식의 의미가 무엇이냐?
해당 식을 풀 수 있다면 모든 운동에 대해서 표현이 가능하단 말이다.
즉, x = At^2 + Bt + C 와 같이 표현이 가능하다는 말이다.
근데.. 적분을 어떻게 할까??
우선 중력에 대해서 알아보자.
a = F/m에서
F = mg
a = g 로 t에 대해 적분 2번하면 나온다.
우선 잘 구해지는 것 같다.
다른 힘은??
용수철에 연결된 물체에 적용되는 힘을 적용해볼까?
F = -kx로 된다.
x가 포함된 식이다.
t로 적분하더라도 x 자체를 구할 수 없어서 풀 수 없다.

음..
그렇다면 x를 없애고 싶다면 어떻게 해야할까??
두 번 적분했을 때 자기 자신으로 돌아가는 함수가 있나?? 생각해보자
자연상수 e^x가 있고... Sin, Cos 이 있는 것 같네??
우선 sin을 이용해볼까??
t에 대해서 표현해보자

A와 w는 상수다.

음..?
결국 x에 대한 식이 조금 비슷해졌다.
w^2 = k/m이라 한다면..
운동방정식과 연립해보자
x가 구해진다.
x = A * sin(root(k/m) * t )가 되는 것이다.
숫자가 더럽지만 맞다.
다시 말하면 위와 같이
2번 적분하거나 우리가 해결할 수 있는 함수로 지정해서 하거나
그렇다고 모든 미분방정식을 풀 수 있다고 보장하진 않는다.
선형 미분 방정식의 경우 반드시 해가 있지만
비선형인 경우 해를 보장하지 않는다.
특히 게임에서는 유체 역햑과 관련된 경우가 그렇다.
유체는 바람도 될 수 있고 물도 될 수 있고 그렇다.
즉, 해를 보장할 수 없으니 우리는 컴퓨터에게.. 어느 정도 우리가 다듬은 값을 전해줘야 한다.
그것이 바로 미분 방정식의 수치 해석이다.
Euler Method라는 것이 있다. 알아보자
오일러 법은 그냥 적분과 비슷한 느낌이다.
테일러 급수에서 유도된 방법으로 오차가 생각보다 큰 방법이다.
요약하자면
직전의 결과로부터 다음 결과를 얻는다는 것이다.
말하자면 근사해이다.

감이 오는게... A0와 A1의 간격이 줄어들면 정확해지지 않을까??
라고 생각하면 맞다.
delta T가 무한히 줄어들면
그게 바로 미분이다.
하지만 우리는 근사해를 얻고자하는 것이다.
왜?? 미분할 수 없어서..ㅎ
위키백과에서 예를 따왔다.
#include <stdio.h>
//초기값을 2로 설정 (y(0)=2)
double y = 2.0;
void EulerMethod(double dt, double t_end) {
// dt는 독립변수 증가량, t_end는 독립변수의 목적지
double dydt;
// 독립변수는 0부터 시작
for (double t = 0;;) {
printf("%.2f \t %.2f\n", t, y);
dydt = 4; // y'=4이므로 y=4x+c. y(0)=2이므로 c=2. 따라서 y=4x+2
y = y + dt * dydt;
if (t_end <= t) {
break;
}
t = t + dt;
}
}
int main(void) {
EulerMethod(0.01, 3); // 0.01 간격으로 3까지 단계적으로 계산
}dt가 바로 간격이 되는 것이고
y가 바로 우리가 구하고자하는 근사해이다.
아무튼 이 간격을 보통 게임에서는 1프레임으로 맞춘다.
오차가 크게 발생하긴 하지만 우리가 게임을 플레이할 때 자연스럽게만 보이면 상관없다.
우리는 실제처럼 구현하고자 하는 것이지 실제와 같이 구현하는 것이 아니기 때문이다.
하지만 더욱 더 높은 정확성을 요구하는 작업을 할 때에는 다른 방법을 쓴다.
1. 1프레임 동안 여러 번 오일러 법 계산 ( 흔히 많이 사용)
2. 선형 근사가 아닌 고차 근사를 사용
3. 다단법, Adams-Bashforth 사용.
그것은.. 필요하면 공부하도록 하자.
'Game Development, 게임개발 > 게임 수학,물리' 카테고리의 다른 글
| 게임 물리 - 원근감의 표현 (0) | 2021.08.22 |
|---|---|
| 게임 물리 - 화면스크롤 (0) | 2021.08.21 |
| 게임 물리 - 원운동 (0) | 2021.08.20 |
| 게임 물리 - 랜덤하게 힘을 적용하기 (0) | 2021.08.20 |
| 게임 물리 - 2가지 이상의 힘이 작용할 때 (0) | 2021.08.19 |