[리뷰/IT] - 처음 시작하는 딥러닝 / 세스 와이드먼 [책리뷰]
https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/
이 분의 저서를 참고했다.
나 책 있다.
딥러닝의 구성은 크게 2가지로 나눌 수 있다.
Neural Network한다면 이렇게 생긴 것을 떠올린다.

우리는 입력에 대하여 층을 거치면서 계산을하고 출력을 발생시킨다.(Forward)
출력에 대하여 Loss 계산을 하고 해당 Loss 함수에 대한 도함수를 구한다.(Backward)
해당 도함수를 이용하여 Loss가 낮은 쪽으로 층을 개선시켜 다음의 입력에서 Loss를 낮추는 것이다.
(Optimizer & Trainer)
한 번 살짝 보자.
Input, Weight, Bias 가 다 나와있다.

계산은 이렇게 한다.

각 입력에 가중치와 편향치를 적용해서 출력을 살펴보면

출력이 나온다.(Forward)
**출력 함수는 Sigmoid 함수이다.

**시그모이드 함수는 미분했을 때, 특별한 결과가 나온다. 찾아보자
하지만 이에 끝나지 않고 해당 출력이 나오는 합성함수의 도함수를 구해야 한다.
가중치를 Loss가 최소로 나오게끔 수정해야하기 때문이다.

하지만 쉽지 않다.
Chain Rule을 적용하여 계산한다.

Backward , Backpropagation은 별 것은 없다.

하지만 중요하다.
우리가 직접 구현할 일은 거의 없지만
정말 질 높은 Tuning을 하기 위해서는 건드려야하는 순간이 올 수도 있다.
때문에 각각의 Forward와 Backward에 대해서 알아볼 필요가 있다.
딥러닝, Deep Learning에는 충분히 많은 요소가 들어간다.
Operation, Layer, Trainer, Optimizer, Bias, Loss, Activate Function 등..
이러한 것들에 대해서 어떤 식으로 쓰이는 가를 공부하고 딥러닝을 시작한다면
모든 것에 대해 감이 올 것이다.
먼저 연산의 기반이 되는 Operation에 대해서 알아보자.
직접적으로 쓰이지는 않으나. 모든 연산에 대해 인터페이스를 제공함으로 상속받은 클래스에서 구현으로써
해당 역할을 한다.
class Operation(object):
"""
신경망 모델에서 연산을 구현하는 클래스 생성
행렬곱이나 bias 를 더하는 작업들을 여기서 추상화해서 사용하겠다는 말이다.
연산은 기본적으로 Forward와 Backward가 있다.
Input, Output이 구현되어 있으나 실제로 실행되는 것은 _output(), _input_grad()임
"""
def __init__(self):
pass
def forward(self, input_: ndarray):
"""
인스턴스 변수에 입력 받은 것을 저장 후 output() 호출
해당 출력값을 return 한다.
"""
self.input_ = input_
self.output = self._output()
return self.output
def backward(self, output_grad: ndarray):
"""
self._input_grad()를 호출한다.
출력에 대한 기울기를 담은 ndarray와 출력 ndarray는 shape가 같아야 한다.
"""
#해당 부분 -> shape가 같아야함.
assert_same_shape(self.output, output_grad)
self.input_grad = self._input_grad(output_grad)
# 입력과 입력에 대한 기울기를 담은 것도 마찬가지다. -> shape가 같아야함.
assert_same_shape(self.input_, self.input_grad)
return self.input_grad
def _output(self):
#Operation과 같은 추상클래스에게 상속 받으면 구현해야 하는 부분. 오버라이딩이라고 보면 되겠다.
raise NotImplementedError()
def _input_grad(self, output_grad):
raise NotImplementedError()
우리가 알고 있는 일반적인 연산으로는
Weight와의 행렬곱, Bias에 대한 편향값 합, 활성화함수가 있다.
이 외에도 우리가 만드려는 모델에 따라 더 늘어날 수 있다.
요약하자면
Operation 밑에
(Dot Product, Add Bias, Activation Fuction, ...등이 있다는 것이다.)
**Sigmoid가 가장 기본적인 활성화 함수라 생각해보고 구현해보자
먼저 Weight에 관한 연산
class ParamOperation(Opertaion):
"""
파라미터 연산임 일반적으로 (Weight)와의 관련된 연산
해당 클래스를 상속받아서 구현함.
"""
def __init__(self, param:ndarray):
super().__init__()
self.param = param
def backward(self, output_grad: ndarray):
"""
_input_grad 와 _param_grad를 호출함
객체 모양일치 확인 후 연산
Operation의 backward 오버라이딩
"""
assert_same_shape(self.output, output_grad)
self.input_grad = self._input_grad(output_grad)
self.param_grad = self._param_grad(output_grad)
assert_same_shape(self.intput_, self.input_grad)
assert_same_shape(self.param, self.param_grad)
return self.input_grad
def _param_grad(self, output_grad:ndarray):
"""
추상클래스과 같이 위 메서드를 구현해야함
"""
return NotImplementedError()
실제적으로는 해당 연산이 행렬 곱이라면 Param..을 상속받아 아래와 같이 구현한다.
class WeightMultiply(ParamOpertaion):
"""
신경망의 가중치 행렬곱 연산을 하는 클래스
실제적으로 Param에 관한 연산으로 여기서는 행렬곱으로 쓰임
Layer, WeightMultiply
"""
def __init__(self, W:ndarray):
# param을 W로 초기화
super().__init__(W)
def _output(self):
#input과 param(weight)의 행렬곱 연산 반환
return np.dot(self.input_, self.param)
#output_grad로 intput_grad와 param(weight)에 대한 gradient 계산
def _input_grad(self, output_grad:ndarray):
return np.dot(output_grad, np.transpose(self.param,(1,0)))
def _param_grad(self, output_grad:ndarray):
return np.dot(np.transpose(self.input_, (1,0)), output_grad)
다음으로는 Bias
class BiasAdd(ParamOperation):
"""
Bias, 편향을 더해주는 연산
-> 얘는 바로 쓸 수 있음 Bias는 일반적으로 합연산으로 정해져있음.
"""
def __init__(self, B:ndarray):
#self.param을 B로 초기화하고 행렬의 모양(shape)비교
#열이 1이어야 각 입력에 대해서 bias를 더함.
assert B.shape[0] == 1
super().__init__(B)
#출력값 계산
def _output(self):
return self.input_ + self.param
#입력에 대한 기울기 계산
def _input_grad(self, output_grad:ndarray):
return np.ones_like(self.input_) * output_grad
def _param_grad(self, output_grad:ndarray):
#파라미터에 대한 계산
param_grad = np.ones_like(self.param) * output_grad
return np.sum(param_grad, axis = 0).reshape(1, param_grad.shape[1])
다음은 활성화함수
class Sigmoid(Opertaion):
"""
활성화 함수 중 하나를 구현 -> 얘는 바로 쓸 수 있음.
Operation을 받아서 바로 구현한 것임.
"""
def __init__(self):
super().__init__
def _output(self):
return 1.0/(1.0 + np.exp(-1.0 * self.input_))
def _input_grad(self, output_grad: ndarray):
sigmoid_backward = self._output * (1.0-self._output)
_input_grad = sigmoid_backward * output_grad
return input_grad
class Linear(Operation):
'''
항등 활성화 함수
'''
def __init__(self) -> None:
super().__init__()
def _output(self) -> ndarray:
#입력에 관해서 그대로 출력
return self.input_
def _input_grad(self, output_grad: ndarray) -> ndarray:
#그냥 그대로 출력
return output_grad
다음으로는
Layer에 관해서다.
Layer에서 무엇을 해야하길래 따로 구현을 해야하느냐?
Layer에서 각 층에서 어떤 연산을 수행해야 하며
각 층에서 어떤 Weight를 갖고 할 것이며
각 층에서 나온 출력 값을 저장해야하는지
등등이 있다.
결국 Operation을 구성한 것도 Layer를 구성하기 위한 것이라고 볼 수 있다.
class Layer(object):
#신경망 모델의 Layer(층)을 꾸밈.
def __init__(self, neurons: int):
"""
뉴런의 개수가 곧 층의 너비를 뜻함
params -> Weight 각 층에 결과 저장
param_grads -> 도함수 각 층에 결과 저장
operation -> 각 층에서 수행할 Operation 저장
"""
self.neurons = neurons
self.first = True
self.params: List[ndarray] = []
self.param_grads: List[ndarray] = []
self.operations: List[Operation] = []
def _setup_layer(self, num_in : int):
#Layer를 구성하는 클래스에서 구현
return NotImplementedError()
#Layer에 값을 입력받고 각 층에서 이루어질 Operation을 수행해서 Output을 반환
def forward(self, input_:ndarray):
"""
입력 값을 받아서 순방향 계산 수행 -> foward
"""
#최초 입력값 받기
if self.first:
self._setup_layer(input_)
self.first = False # -> 다시는 실행되지 않게 만듬
#해당 입력을 input에 저장
self.input = input_
#최초입력값으로 연속적으로 operation 수행
for operation in self.operations:
input_ = operation.forward(input_)
#모든 operations을 수행한 값 = 결괏값
self.output = input_
return self.output
#output_grad를 입력받아서 수행 (output_grad는 다른 곳에서 구함)
def backward(self, output_grad: ndarray):
"""
output_grad를 역순으로 통과시켜서 계산 수행 <-
하지만 연산하기 전 shape 검사를 해야함.
"""
assert_same_shape(self.output, output_grad)
#Forawrd에서 수행했던 연산을 역순으로 grad를 구하는데 수행함.
for operation in reversed(self.operations):
output_grad = operation.backward(output_grad) # -> 이때의 backward는 operation의 backward()함수임
#최종적으로 수행한 값은 Loss의 기울기 일 것임.
input_grad = output_grad
self._param_grad()
return input_grad
def _param_grad(self):
#각 operation 에서 _param_grad 값을 구함
self.param_grads = []
for operation in self.operations:
#해당 인스턴스가 ParamOperation의 subclass라면
if issubclass(operation.__class__, ParamOperation):
self.param_grads.append(operation.param_grad) # -> 여기서도 param_grad는 Operation의 param_grad임
def _param(self):
#각 operation에서 _param 값을 구함
self.params = []
for operation in self.operations:
if issubclass(operation.__class__, ParamOperation):
self.params.append(operation.param)
그럼 해당 Layer에 대해서 어떻게 적용을 해야하느냐..?
그래서 전결합층을 만들기 위해 Dense를 구현했다.
class Dense(Layer):
#Layer 클래스를 상속받아 구현
#여기선 기본 활성화함수를 시그모이드로 함 -> 바꾸기 가능
def __init__(self,
neurons:int,
activation: Operation = Sigmoid()):
#초기화 시 Activation Function 결정
super().__init__(neurons)
self.activation = activation
def _setup_layer(self, input_: ndarray):
#전결합층 -> 행렬곱을 의미.
#n1개의 행과 n2개의 열이 있을 때
#행렬곱 계산을 한다면 n1개의 최초특징 가중합으로 계산된 n2개의 새로운 특징을 만들어낸다고 이해하면 된다.
#모두가 이러한 계산을 하지는 않음 Ex) CNN 은 입력 특징의 일부만 조합하는 것이다.
if self.seed:
np.random.seed(self.seed)
self.params = []
#Weight -> input의 열 * neuron의 개수(행)만큼의 (0~1)의 범위의 matrix 반환 (임의의 가중치)
self.params.append(np.random.randn(input_shape[1], self.neurons))
#Bias -> 1행 neurons의 값의 열 만큼에 0~1까지의 matrix 반환. (임의의 편향값)
self.params.append(np.random.randn(1,self.neurons))
#위에서 넣은 원소를 바탕으로 activation 수행
self.operations = [WeightMultiply(self.params[0]),
BiasAd(self.params[1]),
self.activation]
return None
다음으로는 Loss에 대해서 조사를 해야한다.
Loss를 전역 최소로 하는 값을 향해 우리가 각 수치들을 조정해야하기 때문이다.
Loss Function도 여러가지가 존재하기 때문에
기본적인 Loss class를 구성 후 상속받아 구현한다.
class loss(object):
#손실을 계산함
def __init__(self):
pass
#Loss는 예측한 값과 실제 값의 다른 정도로 계산된다.
def forward(self, prediction:ndarray, target:ndarray):
#실제 손실 값 계산
assert_name_shape(prediction, target)
self.prediction = prediction
self.target = target
loss_value = self._output()
return loss_value
#손심 함수의 입력값에 대한 손실함수 기울기
def backward(self):
self.input_grad = self._input_grad()
assert_same_shape(self.prediction, self.input_grad)
return self.input_grad
#아래 함수들은 어떻게 Loss를 구할 것인지. 어떤 함수를 Loss로 할 것인지에 달림
def _output(self):
#Loss 클래스를 상속받아 구현
raise NotImplementedError()
def _input_grad(self):
#Loss 클래스를 상속받아 구현
raise NotImplementedError()
대표적으로 MSE, MeanSquareError로 구현해보겠다.
class MeanSqauredError(Loss):
def __init__(self):
super().__init__()
#MSE에서는 예측 값과 실제 값의 차이를 제곱한 것을 평균을 낸다.
def _output(self):
#합을 행의 수로 나눔
loss = (
np.sum(np.power(self.prediction - self.target, 2)) /
self.prediction.shape[0]
)
return loss
#위와 같이 구현
def _input_grad(self):
return 2.0 * (self.prediction - self.target) / self.prediction.shape[0]
다음으로는 Neural Network로
각 연산이 합쳐서 층을 이루고
층이 합쳐서 결국 신경망 자체를 이루게 된다. 이에 대해서 구현해보자
class NeuralNetwork(object):
'''
신경망을 나타내는 클래스 실제로 Layer 구성과 Loss function 등으로 이루어짐.
'''
def __init__(self,
layers: List[Layer],
loss: Loss,
seed: int = 1) -> None:
'''
신경망의 층과 손실함수를 정의
'''
self.layers = layers
self.loss = loss
self.seed = seed
if seed:
for layer in self.layers:
setattr(layer, "seed", self.seed)
#배치만큼씩 데이터를 집어넣음.
def forward(self, x_batch: ndarray) -> ndarray:
'''
데이터를 각 층에 순서대로 통과시킴(순방향 계산)
'''
x_out = x_batch
for layer in self.layers:
x_out = layer.forward(x_out) #얘는 Layer의 forward함수임
return x_out
# loss_grad를 레이어 역순으로 집어넣음.
def backward(self, loss_grad: ndarray) -> None:
'''
데이터를 각 층에 역순으로 통과시킴(역방향 계산)
'''
grad = loss_grad
for layer in reversed(self.layers):
grad = layer.backward(grad) # Layer의 backward 함수임을 알자.
return None
# x가 실제로 넣어서 예측된 값이고 y가 정답값
def train_batch(self,
x_batch: ndarray,
y_batch: ndarray) -> float:
'''
순방향 계산 수행
손실값 계산
역방향 계산 수행
'''
predictions = self.forward(x_batch)
#정답값을 이용하여 Loss 적용
loss = self.loss.forward(predictions, y_batch)
#정답 값을 이용하여 Loss grad 적용
self.backward(self.loss.backward())
return loss
def params(self):
'''
신경망의 파라미터 값을 받음
'''
for layer in self.layers:
yield from layer.params # Layer의 params를 받음.
def param_grads(self):
'''
신경망의 각 파라미터에 대한 손실값의 기울기를 받음
'''
for layer in self.layers:
yield from layer.param_grads # Layer의 param_grad를 받음
결국 이렇게 된다면 Loss function으로 기울기를 구해서
전역 최소 값을 가질 수 있도록 weight나 bias를 변화시켜야 한다.
우리가 원하는 학습이 이것이다.
그것을 여기선 Optimizer라고 한다.
class Optimizer(object):
'''
신경망을 최적화하는 기능을 제공하는 추상 클래스 -> Optimizer는 여러가지로 이 클래스를 상속받아 만든다.
'''
def __init__(self,
lr: float = 0.01):
'''
초기 학습률이 반드시 설정되어야 한다. #시작 시 하이퍼파라미터로 입력됨.
'''
self.lr = lr
def step(self) -> None:
'''
Optimizer를 구현하는 구상 클래스는 이 메서드를 구현해야 한다.
'''
pass
이렇게 보면 감이 안오겠지만
실제로 많이 쓰이는 SGD,Stochastic Gradient Descent 으로 확률적 경사 하강법이란
이름의 Optimizer가 흔하게 쓰인다.
class SGD(Optimizer):
'''
확률적 경사 하강법을 적용한 Optimizer
'''
def __init__(self,
lr: float = 0.01) -> None:
'''Pass'''
super().__init__(lr)
def step(self):
'''
각 파라미터에 학습률을 곱해 기울기 방향으로 수정함
'''
#다시 말해서 param을 꺼내고 그 해당하는 param에 대한 기울기를 구해서 최소 값을 가도록 함수좌표 상에서 lr 만큼 이동시킨다 라고 생각하면 된다.
#여기서 net은 neural network를 말한다.
for (param, param_grad) in zip(self.net.params(),
self.net.param_grads()):
param -= self.lr * param_grad
마지막으로는
이것들을 순차적으로 모든 데이터에 대해서 수행시켜 모델을 학습시키는 클래스인
Trainer를 만들어야 한다.
우리가 실제로 쓴다고 생각하는 것이 바로 이것이다.
살펴보자
from copy import deepcopy
from typing import Tuple
class Trainer(object):
'''
신경망 모델을 학습시키는 역할을 수행함
실제로 우리가 쓴다고 생각하면 된다.
'''
def __init__(self,
net: NeuralNetwork,
optim: Optimizer) -> None:
'''
학습을 수행하려면 NeuralNetwork, Optimizer 객체가 필요함 -> 배운 것중 가장 상위에 위치한다고 생각하면 된다.
Optimizer 객체의 인스턴스 변수로 NeuralNetwork 객체를 전달할 것 -> 그래서 Optimizer에서 net이 쓰임.
'''
self.net = net
self.optim = optim
self.best_loss = 1e9
setattr(self.optim, 'net', self.net)
#배치를 생성하여 -> 나눈다고 생각하면 된다.
def generate_batches(self,
X: ndarray,
y: ndarray,
size: int = 32) -> Tuple[ndarray]:
'''
배치 생성
'''
assert X.shape[0] == y.shape[0], \.format(X.shape[0], y.shape[0])
'''
특징과 목푯값은 행의 수가 같아야 하는데,
특징은 {0}행, 목푯값은 {1}행이다
'''
N = X.shape[0]
#N씩 끊어서 만듬
for ii in range(0, N, size):
X_batch, y_batch = X[ii:ii+size], y[ii:ii+size]
yield X_batch, y_batch
#epoch -> 전체 데이터를 순회함 1epoch는 한 번 전체 데이터 순회
#train으로 학습하고 test로 성능 측정함.
def fit(self, X_train: ndarray, y_train: ndarray,
X_test: ndarray, y_test: ndarray,
epochs: int=100,
eval_every: int=10,
batch_size: int=32,
seed: int = 1,
restart: bool = True)-> None:
'''
일정 횟수의 epoch을 수행하며 학습 데이터에 신경망을 최적화함
eval_every 변수에 설정된 횟수의 매 에폭마다 테스트 데이터로
신경망의 예측 성능을 측정함
'''
np.random.seed(seed)
if restart:
for layer in self.net.layers:
layer.first = True
self.best_loss = 1e9
for e in range(epochs):
if (e+1) % eval_every == 0:
# 조기 종료
last_model = deepcopy(self.net)
X_train, y_train = permute_data(X_train, y_train)
#배치를 생성하여 수행
batch_generator = self.generate_batches(X_train, y_train,
batch_size)
#미니 배치 사이즈마다 Optimize로 가중치 수정 -> 업데이트
for ii, (X_batch, y_batch) in enumerate(batch_generator):
self.net.train_batch(X_batch, y_batch)
self.optim.step()
#eval = evaluation, 측정을 말함.
if (e+1) % eval_every == 0:
#test 데이터에 대해 forward 계산 후 loss 계산
test_preds = self.net.forward(X_test)
loss = self.net.loss.forward(test_preds, y_test)
# 업데이트 된 모델이 loss가 작아졌다면 그대로 업데이트
# 반대로 loss가 커졌다면 다시 이전 모델을 가져옴.
if loss < self.best_loss:
print(f"{e+1} 에폭에서 검증 데이터에 대한 손실값: {loss:.3f}")
self.best_loss = loss
else:
print(f"""{e+1}에폭에서 손실값이 증가했다. 마지막으로 측정한 손실값은 {e+1-eval_every}에폭까지 학습된 모델에서 계산된 {self.best_loss:.3f}이다.""")
self.net = last_model
# self.optim이 self.net을 수정하도록 다시 설정
setattr(self.optim, 'net', self.net)
break
이제 거의 다 알아봤다.
그래서 한 눈에 구성하는 방법을 알 수 있게 내가 파워포인트를 이용해보겠다.
파란색이 주요한 클래스고
초록색이 얼마든지 커스터마이징 가능한 부분이다.
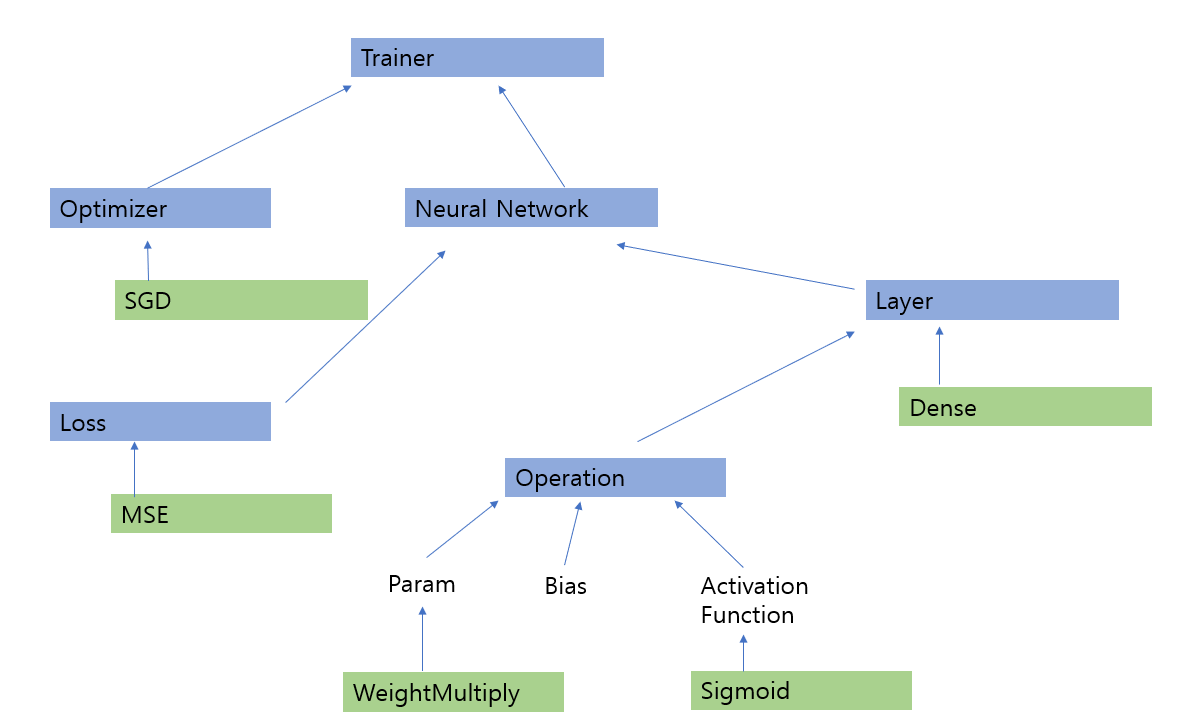
딥러닝은 위와 같은 구성으로 되어있고
우리가 Forward와 Backward를 안다면 어떤 모델을 만들어 평가할 것인지는 각자의 손에 달려있다.
또한 이러한 구조를 알고 있다면 기존의 모델도 튜닝이 가능하니까 딥러닝을 이용하기만 한다는 생각은 버리자.
있는 것도 나에게 맞게 활용할 수 있는 것이 정말 딥러닝을 배우는 길일 것이다.
'데이터 사이언스(Data Science) > ML&DL' 카테고리의 다른 글
| 퍼셉트론으로 결정경계 생성, Perceptron (2) | 2021.12.07 |
|---|---|
| K-Means 프로젝트, Unsupervised Learning (1) | 2021.11.30 |