K-Means 프로젝트, Unsupervised Learning

 

클러스터링 중 가장 유명한 기법으로 

분포되어있는 N-Dimensional data들을 계산할 수 있는 방법이다.

임의의 데이터

좌표 평면이라면 사람이라도 어느 정도 클러스터링이 가능하겠지만

이것의 진가는 N차원일 때 드러난다.

 

실제로 몇가지 입력으로 실험해봤다.

 

 

---

 

크게 5가지로 나누어서 실행했다.

1) Data loading cell

2) findClosestCentroids function cell

입력데이터 X (m x n) 와 K개의 중앙점 위치 c (K x n)가 주어졌을 때, 각 입력데이터가 몇번째 중앙점과 가장 가까운지 계산하여 idx 로 반환한다. 이때 idx는 m-dimensional vector이며 0에서 K-1 사이의 인덱스로 이루어져있다.

3) computeMeans function cell

입력데이터 X (m x n), 각 입력데이터가 몇번째 cluster에 속하는지에 대한 정보 idx (m x 1), cluster의 갯수 K가 주어졌을 때, 새로운 centroid의 위치를 계산하여 c로 반환한다. c는 (K x n)

4) kMeansInitCentroids function cell

제일 처음 입력데이터 X (m x n) 중에서 random하게 K개를 골라 중앙점 c로 반환한다. c는 (K x n)

5) Run cell

실행하였을 때 expected_result.png와 같은 결과를 얻을수 있다. 구현의 편의를 위하여, converge 조건을 따로 정하지 않고, iteration을 30번 수행하면 loop이 끝나도록 구현

 

 

---

 

# 1.Data loading
data_path = #임의의 경로
data = #임의의 데이터
X = data['X']
plt.scatter(X[:,0],X[:,1],c='b')
plt.grid(True)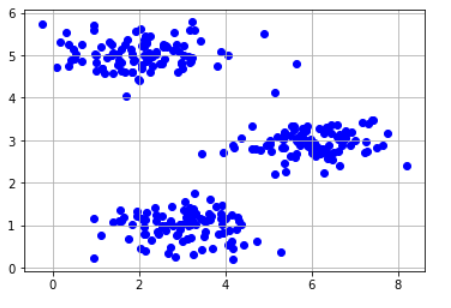

 

# 2. X(좌표상의 점) c(cetroids)
# n차원의 정보 m개
# n차원의 centroids K개
# idx도 결국 m개 -> m개에 대한 가장 가까운 centroids 반환
def findClosestCentroids(X, c):
  m, n = np.shape(X)
  K, n = np.shape(c)  
  idx = -1*np.ones(m) # Initialization [-1,-1,......-1] m개

  for i in range(m):
    distances = np.zeros(K)
    for j in range(K):
      distances[j] = np.sqrt(((X[i,:]-c[j,:])**2).sum(axis = 0)) #각 차원에 대한 차 제곱에 대한 합 제곱근
    
    idx[i] = np.argmin(distances) #X 값의 i번째 입력데이터에 대한 가장 작은 값을 가지는 index 를 반환함
  return idx

# 3
# X 입력데이터, idx 입력데이터 순서에 따른 가장 작은 K centroids 번호, K cetroids 목록
def computeMeans(X, idx, K):
  m, n = np.shape(X)
  c = np.zeros((K,n)) #K개의 n차원

  for i in range(K): #K.shape(0) == K개
    #해당 클러스터 번호에 대한 X의 번호를 골라냄
    #해당 번호에 대한 X의 mean을 구함
    c[i] = np.array(X[idx == i].mean(axis = 0))

  return c

# 4.
def kMeansInitCentroids(X, K):
  m, n = np.shape(X)

  centroids = X.copy() #현재 포인트들 중에서 랜덤으로 K개 뽑음
  np.random.shuffle(centroids) #섞은 후 앞에서 3개뽑음
  c = centroids[:K]
  return c

# 5. Run K-means

# 임의로 바꿀 수 있음
iterations = 30
K=3
centroids = kMeansInitCentroids(X, K)



#iteration 만큼 K 좌표를 바꾸면서 찾아감
for i in range(0,iterations):
  idx = findClosestCentroids(X, centroids)
  centroids = computeMeans(X, idx, K)

#실제 실행된 결과
cmap = plt.cm.get_cmap('hsv', K+1)
for j in range(0,K):
  assigned_idx = np.where(idx==j)
  dim, num = np.shape(assigned_idx)
  assigned_idx = np.reshape(assigned_idx,num)
  
  plt.scatter(X[assigned_idx,0],X[assigned_idx,1],c=cmap(j))
  plt.scatter(centroids[j,0],centroids[j,1],c='k',marker='x')
plt.axis('equal')
plt.grid(True)

 

 

---

 

Iteration을 하면서 움직이는 정도가 Mean이 괜찮은지?

-> Learning rate 처럼 크거나 작아서 Global하지 못하고 Local한 해답을 찾을 수 있을 것이라 생각했지만

찾아보니 실제로 Local 한 해답을 내놓았다. 

하지만 K-means 자체는 언레이블된 것들에 대해서 다시 레이블링해줄 수 있다는 것에 큰 역할을 했기 때문에 쓸만했다.

 

Iteration을 많이할수록 좋은지?

-> 실제로 유사 최적해를 내놓았다. Loss가 점차 줄어드는 것은 부정할 수 없다.

하지만 Loss 개선율이 낮아지므로 최적의 Loss보다는 최적의 Iteration을 찾아내는 것이 더 적합할 수 있다.