퍼셉트론으로 임의의 포인트들에 대하여 이진 분류하고자 한다.
numpy 와 pyplot만 이용해서 구현할 생각이다.
임의의 점과 레이블 설정

한 번 주어진 포인트에 대해서 시각화를 해보았다.

그런대로 잘 나왔다.
이제 결정경계를 만들기 위해서
임의로 가중치를 정해서 결정경계를 만들어보자
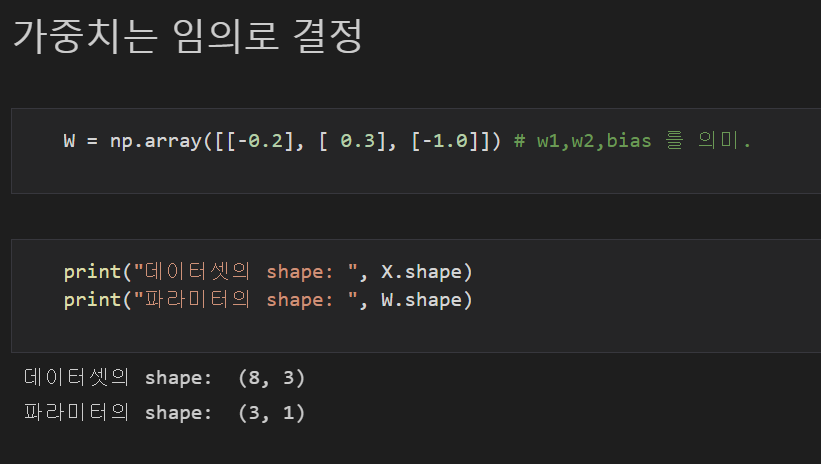
가중치로 만든 결정경계 직선을 그리는 함수를 만들었다.
입력은 가중치(np.ndarray(1,3)을 받는다.
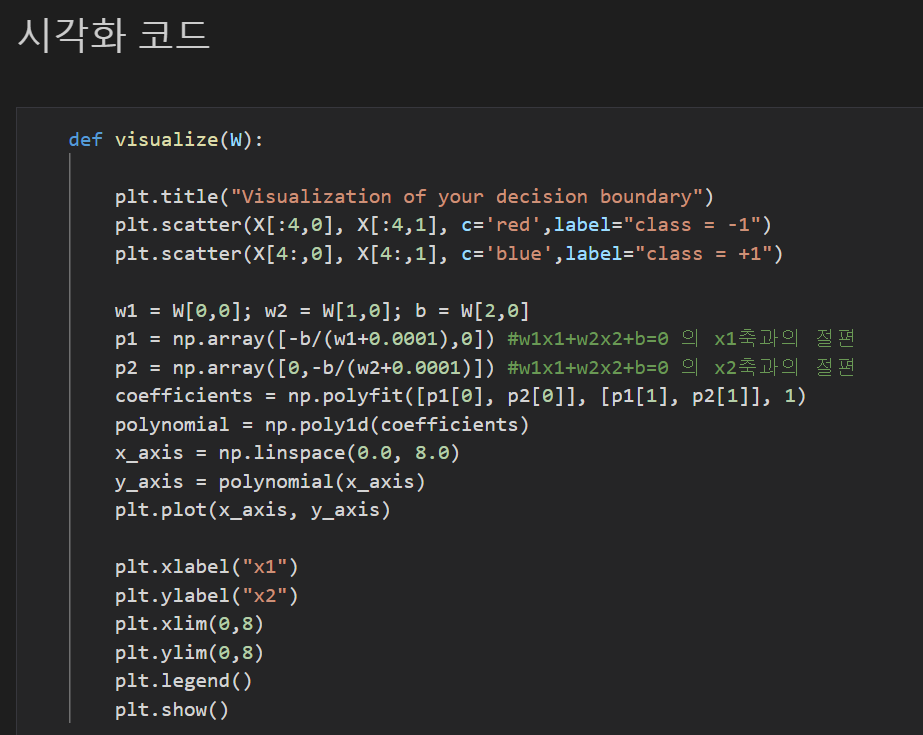
주어진 임의의 가중치가 어떻게 그려지나 한 번 살펴봤다.
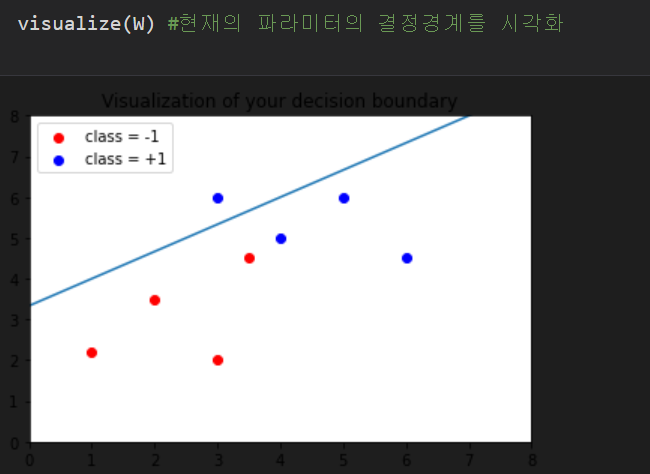
이제는 퍼셉트론의 원리를 이용해서 가중치 곱에 대한 합을 기준으로 분류를 하고 다르다면 해당 결정경계를 업데이트 하는 방식으로 진행할 예정이다.
Perceptron은 learning rate 와 iteration 수, threshold를 결정하여 클래스를 구분하며 얼마나 업데이트할 것이며 학습을 몇번 시킬지가 결정된다.
ㅇ이것은 코드로 직접 넣었다.
#퍼셉트론 정의
class Perceptron():
#임계값, leraning rate, iteration 수
def __init__(self, thresholds=0.0, eta= 0.05, n_iter = 20000):
self.thresholds = thresholds #기준 값
self.eta = eta #learning rate
self.n_iter = n_iter #학습 횟수
#트레이닝 데이터 X와 y를 레이블로해서 머신러닝 수행
def fit(self, X, y, W):
self.w_ = copy.deepcopy(W) #기본 가중치[w1,w2,b]
#n_iter 만큼 반복
for _ in range(self.n_iter):
#X의 [x1,x2,w]와 y에서 [y]값을 뽑아냄
for xi, target in zip(X,y):
#learning rate 만큼 수정
update = self.eta * (target - self.predict(xi))
#해당 update만큼 가중치 조정
xi = np.reshape(xi, (3,1))
self.w_ += update * xi
return self
#벡터 해당 행렬과 가중치의 곱의 합 -> (모든 데이터에 대한)
def net_input(self, X):
return np.matmul(X,self.w_) # x1*w1 + x2*w2 + 1*b
#가중치 곱의 합이 threshold보다 큰지 작은지
def predict(self, X):
return np.where(self.net_input(X)[0] > self.thresholds, 1, -1)
결과는 만족스럽게 나왔다.
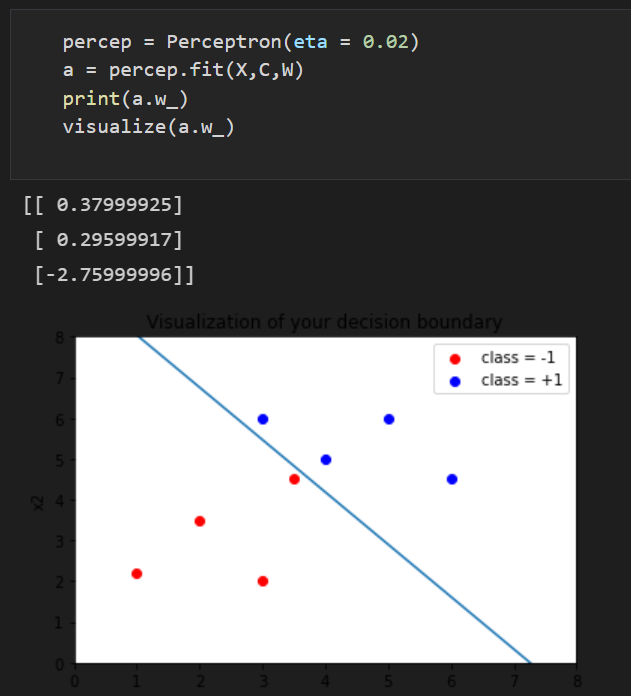
하지만 왜 나왔는지도 모르고 하는 것은 정말 몰랐을 때고
했으니까 이제는 왜 저렇게 이진 분류가 가능한 지를 알아봐야 한다.
퍼셉트론의 출력을 먼저 보자
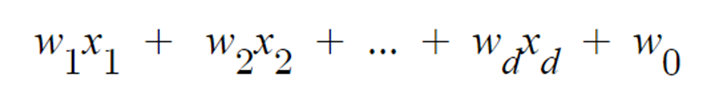
이전에 나온 퍼셉트론의 출력에서는 x1,x2항만을 가져 직선의 방정식이 되는 것을 알 수 있다.
하지만 식을 다시보면 (x1,x2,1) 과 (w1,w2,b)와의 내적이란 것을 알 수 있다.
내적은 벡터의 개념이 사라지고 스칼라로 바뀐다.
즉, 내적은 두 벡터의 관계 정도로 해석되는데
하지만 포인트는 고정되어 있지만 가중치는 계속 업데이트 된다.
고정벡터와 가변벡터에 대한 내적의 의미란
고정 벡터에 대해서 가변벡터가 얼만큼 작용할 수 있느냐 하는 정도를 나타낸다.
즉, 상관도를 나타낼 수 있는데 이를 활용하여 분류하는 것이다.
그렇다면 퍼셉트론으로 분류하는 것이 얼마나 정확한가???
사실 퍼셉트론은 학습을 많이한다고 좋아지는 것은 아니다.
실제로 learning rate와 iteration 의 크기에 좌우되는 것은 아니며
다른 분류알고리즘과 다르게 정확도가 수렴하지 않으며 어느정도의 폭을 가지고 진동하는 형태를 띈다.

때문에 퍼셉트론으로 분류하는 것이 그렇게 정확하다고 할 수는 없으나 단일 층으로 구분하는 경우 이것보다 간단한 분류 알고리즘이 없다고 봐도 무방하다.
'데이터 사이언스(Data Science) > ML&DL' 카테고리의 다른 글
| K-Means 프로젝트, Unsupervised Learning (1) | 2021.11.30 |
|---|---|
| Deep Learning, 딥러닝의 구성 (0) | 2021.09.18 |