//21.12.17 업데이트
회전에 관해서 오일러와 쿼터니언이 있다.
우리가 상식으로 알고 있는 것은 오일러이고
오일러를 보완하기 나온 것이 쿼터니언이다.
알아보자
이해하기 위해선 복소수를 알고 가야 한다.
정의부터 해보자
오일러는 무엇이고
쿼터니언은 무엇인가
오일러는 우리가 알고 있는 상식대로의 rotation이다. X,Y,Z 축이 있고
이 3축에 대해 회전을 표현하는 것이다.
하지만 이렇게 X,Y,Z로 회전을 표현할 수 있다면 쿼터니언의 필요성을 못느꼈을 것이다.
단순히 각 축에 대해서 세 개의 각도를 지정하는 것만으로는 회전이 고유하게 정해지지 않는다.
더군다나 회전행렬에 대해 교환법칙이 성립하지 않는 경우를 봤기때문에 더 그렇다.
-> 즉, 회전시키는 순서가 다르면 해당 각을 똑같이 돌리더라도 결과가 다르게 나오는 경우가 생긴다.
오일러로 회전을 표현하는 것의 한계는짐벌락에 빠진다는 것에 있다.
**짐벌락이란 어느 한 축의 회전이 다른 축에 영향을 주는 것을 말한다.
-> 좀 더 정확하게 말하자면 어떠한 축이 다른 축과 겹쳐져 하나의 성분을 잃고 차원이 낮아지는 것을 말한다.
아래 그림을 보면 성분이 사라졌다는 느낌을 알 것이다.

쿼터니언으로 표현했을 때 이러한 짐벌락 현상을 막을 수 있다.
우선 오일러각으로 3회의 회전을 한다고 해도
회전 행렬을 사용해서 회전할 경우에는 3회의 회전 시점에서 짐벌락이 다시 발생할 때,
다른 회전 행렬을 합성하면 된다. 그래서 짐벌락이 문제가 되지는 않는다.
-> 이 말은 짐벌락에 고리가 4개가 있는 것과 같다.
다만 행렬로 다룰 경우에는 행렬 계산 자체의 부작용이 생긴다.
먼저 부동소수점 연산 오차다.
회전 행렬을 사용하는 경우, 어떤 회전 상태의 모델에 뒤에서부터 여러 번 연속으로 회전을 더해가면,
그때마다 오일러각을 삼각함수에 지정한 결과로서의 float형 수치를 요소로 하는 행렬과의 곱셈이 이뤄진다.
즉, 삼각함수 처리 부하도 무거운데 32비트로 이루어진 부동소수점의 오차가 계산할수록 누적된다는 말이다.
두 번째로는 3D모델 자체에서도 대량의 회전이 필요한데
회전별로 각각 생성한 회전 행렬자체가 부담이 엄청나게 커진다.
마지막으로 축이 다른 두 개의 회전 행렬이 있을 때,
한 쪽 회전에서 다른 쪽 회전으로 매끄럽게 이동해가는 보간(interpolation)은 회전 행렬을 이용하여 표현할 수 없다.
이러한 단점을 이기고자 나온 것이 바로 사원수이다.
아래 바로 쿼터니언이 있다.

** 왜?? 막을 수 있는데..? 4개로 표현하면 뭐가 바뀌는데??
선형대수학을 공부하면 좋다 ㅎㅎ 나중에 내가 더 잘 공부해서 글을 써보겠다.
공학자는 이용을 -> 나
수학자는 증명을 -> 나는 아님
우선 쿼터니언은 오일러보다 연산이 빠르며 정확도도 오일러보다 높다.
짐벌락이 발생하지 않는다.
행렬보다 점유 메모리 영역이 작고 계산 부하가 낮다.
임의의 축에서도 회전을 손쉽게 할 수 있다.(x,y,z를 제외한 임의의 축)
오차가 쉽게 발생하지 않는다.
두 개 회전 사이의 매끄러운 보간(Lerp) 표현 가능
-> 실제로 우리가 오일러 값으로 조정하지만 엔진 내부에서의 계산은 쿼터니언이라고 한다.
복소수로 2차원 평면상의 위치를 나타낼 수 있는 것처럼
3차원에서도 공간 내의 좌표를 표현할 수 있는 세 개의 실수를 발견하고자 했다.
복소수처럼 다룰 수 있는 3개의 실수를 이용하고자 했으나 실패해서
좌절하던 찰나에 네 개의 실수를 이용하면(교환법칙 성립 x)
곱셈과 나눗셈을 정의할 수 있다는 사실을 알아냈고
이를 복소수 한 개의 실수와 허수 단위 i를 조합하여 사용했지만
사원수에서는 네 개의 기저를 사용한다.
사원수 q는 네 개의 기저를 사용한다.(1, i, j, k)
실수 1과 허수 i, j, k 이다.
또한 실수 w, x, y, z 를 이용하였다.
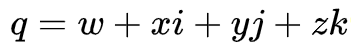
여기서 x = y = z = 0 일 때
사원수 q는 실수가 되고
w = 0 일 때 순허수가 된다.
또한 w를 스칼라부, scalar part
i, j, k 는 벡터부, vector part 라고 한다.
이는 4개의 선형 독립인 기저벡터로 4차원 공간을 말한다.
실수가 아닌 기저 i, j, k 는 특별한 관계가 있는데
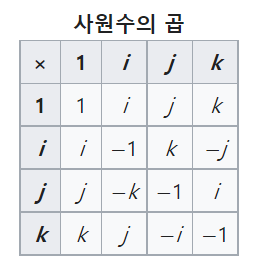
위의 관계를 만족한다.
참고로 i * j * k = -1 이다.
보면 알듯이 교환법칙은 성립하지 않는다.
곱하는 순서를 바꿔버리면 부호가 바뀐다.
** 이러한 성질은 벡터의 외적과 비슷하다.
또한 스칼라부와 벡터부를 나누어 표현하기도 하는데
일반적으로 아래와 같이 표현한다.
q = [s v]
사원수를 정의했으면 사원수 간의 무슨 연산이 되는지 알아봐야겠지?
1. 스칼라배
사원수 q에 대해 스칼라 n을 곱하면 된다.
n * q = [n*s n*v]
2. 공액
복소수에서 켤레복소수가 부호만 바꿔서 존재하는 것처럼여기서도 존재한다.
**벡터부의 부호만 바꾼다.
q = [s v]
q' = [s -v]
3. 크기
복소수에서 크기를 구하듯이사원수도 크기(노름)을 구할 수 있다.
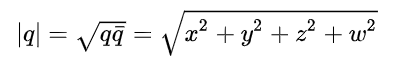
4. 곱셈
사원수들 간의 곱셈도 가능하다.
벡터부의 내적과 외적을 이용해서 정의된다.
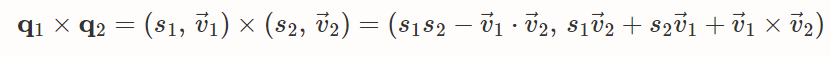
5. 단위 사원수
자신을 연산하면 다시 자신이 나오는 것이 있다.
즉, 크기를 구했을 때 1이 나오는 정규화된 사원수를 단위 사원수라고 한다.
6. 내적
q0 = [s0 v0]
q1 = [s1 v1]
q0 · q1 = s0 s1 + v0 v1
다른 내적과 비슷하게
q · q = |q|^2
..이외에도 역수,행렬로도 표현할 수 있다.
그렇다면 이런 사원수가 어떻게 3D 공간에서 회전을 표현할 수 있다는 것일까?
사원수에서 회전의 대상이 되는 것은 3차원 벡터이다.
여기서 좌표를 변환할 때 벡터를 열벡터로 하여 행렬로 나타내고 행렬의 연산을 적용한 것처럼
3차원인 벡터를 사원수로 나타내야만 한다.
사원수에는 마침 벡터부라고 불리는 부분이 있어서 3차원인 벡터성분을 그곳에 넣고
순 허수 사원수 p = [0 v]로 사용해보자.
어떤 임의의 벡터 p에 대해 단위 사원수 q를 이용해서 3차원 공간에서 회전시켜 벡터 p'를 구해보자
p' = q p q^(-1)
++q^(-1)을 q의 역수를 뜻한다.
또한 q는 단위 사원수 이므로 q의 역수는 q*(공액)와 같다.
??? 아니 근데.. 왜 이렇게 하는거야???
여기서는 사원수를 3차원 공간에서의 회전에 사용하지만 사원수 자체는 3차원 내의 축을 중심으로하는 평면상에서만 회전하는 것이 아니라 4차원으로 직교하는 두 개의 평면 상에서 같은 각도(등각, isoclinic)로 회전한다.
3차원 회전에는 단지 하나의 회전축이 있어 대응하는 하나의 평면 위를 회전했지만
4차원에서는 회전축이라는 것은 없고 원점만 공유하는 두 개의 회전면이 있다.
그래서 왼쪽부터 사원수를 한 번 곱한 단계 : ( q p )
에서는 우리가 만드려는 벡터인 p' 가 3차원 공간 밖으로 나온 상태가 된다. (스칼라배가 0이 아닌 상태)
다시 4차원상에서는 역방향 회전이 되지만, 3차원에서는 최초의 회전과 같은 방향이 되는 회전을 오른쪽부터 더하여 4차원에서의 회전을 없애는 것이다.
3차원 공간으로 벡터 p'를 되돌리고, 스칼라배를 0으로 해서 순허수 사원수로 3차원 벡터라고 볼 수 있는 상태로 복귀시켜야 한다.
위 식이 정말 회전을 나타내는 것이 맞는지??
확인해보자
q = [qs qv]
p = [0 pv]
p' = [s v]
라고 해보자
p' = qpq^(-1)
= [qs qv][0 pv][qs -qv] /// -> 앞 두 사원수의 곱셈
-> p의 실수부가 0이라 벡터부만 남음.
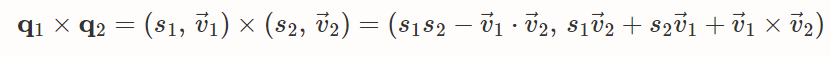
=[-qv · pv qspv + qv x pv][qs -qv] /// -> 다시 사원수의 곱셈
=[ -qs(qv · pv) + qv · (qspv + qv x pv) (qv · pv)qv + qs(qspv + qv x pv) - (qspv + qv x pv) x qv]
우선 p'의 스칼라부를 계산해보자
s = -qs(qv · pv) + qv · (qspv + qv x pv)
= -qs(qv · pv) + qs(qv · pv) + qv · (qv x pv)
= qv · (qv x pv)
스칼라 삼중적으로 나왔다.
하지만 안쪽 2개의 벡터가 같도 선형 종속이기 때문에
s = qv · (qv x pv) = 0
이 나온다.
즉, p'는 실수부가 없는 벡터부만 있는 순허수가 되었고 4차원이 아니라 3차원을 나타내는 것을 알 수 있다.
벡터부도 계산해보자
v = (qv · pv)qv + qs(qspv + qv x pv) - (qspv + qv x pv) x qv...다 정리하면
= (qv · pv)qv + (qs^2)pv + 2qs(qv x pv) - (qv x pv) x qv여기서
(qv x pv) x qv 부분이 벡터의 삼중적이므로 전개하면
v = (qs^2 - qv · qv)pv + 2qs(qv x pv) + 2(qv · pv) qvq는 단위 사원수이므로 qs^2 + |qv|^2 = 1이다.qs^2 = 1 - qv · qv로 표현된다.이를 대입해보면?
v = (qs^2 - qv · qv)pv + 2qs(qv x pv) + 2(qv · pv) qv
= ((1 - qv · qv)- qv · qv)pv + 2qs(qv x pv) + 2(qv · pv) qv
= pv + 2qs(qv xpv) + 2((qv · pv)qv - (qv · qv)pv)
여기서 (qv · pv)qv - (qv · qv)pv 부분이 벡터의 삼중적을 전개한 것이므로다시 전개 전으로 되돌리면
v = pv + 2qs(qv x pv) + 2(qv x (qv x p))가 된다.
즉, 이 식은 오일러 로드리게스의 회전 공식과 완전히 같아진다.
w = v + 2a(e x v) + 2(e x(exv))
즉, 회전변환한 것과 같아지는 벡터부 결과를 얻을 수 있다.
이렇게 회전을 나타내는 사실은 알았지만 회전을 위한 축 q의 벡터는 벡터부의 qv에 설정한다고 해도
아직 회전을 위한 각도를 여기 어디에서 이용하는지 모른다.
그래서 어디에 사용할 지 알아보자
p의 벡터부 pv와 회전 후의 벡터 v의 내적은 pv와 v가 이루는 각도
다시 말해서 실제로 회전축을 중심으로 회전한 각도를 말한다.
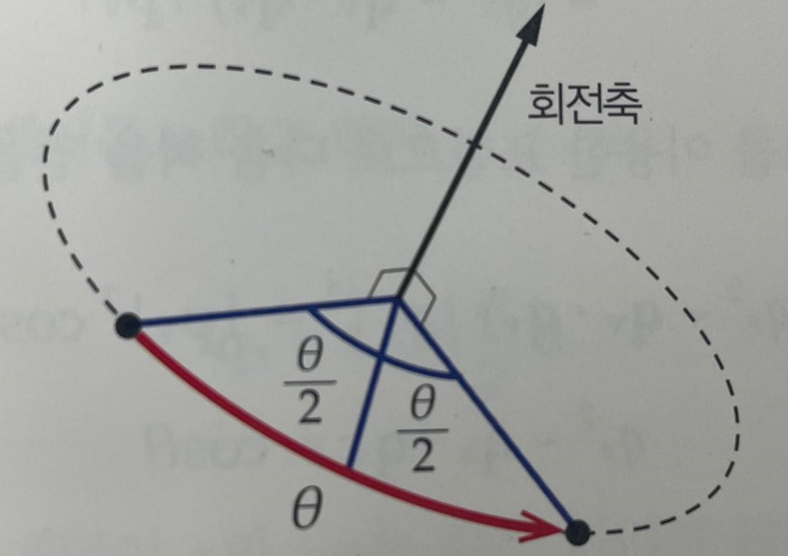
우선은 pv · v를 cosθ로 나타낸다.
pv · v = |pv| |v| cosθ
= |pv|^2 cosθ (|pv| = |v| 이므로)
앞서 구한 v의 식을 이용해서 pv v 를 구해보자
pv · v
=pv · ( pv + 2qs(qv x pv) + 2((qv · pv)qv - (qv · qv)pv))
=pv · pv + 2qs(pv · (qv x pv)) + 2(pv · qv)^2 -2(qv · qv) (pv · pv)
스칼라 삼중적인 pv (qv x pv) 는 pv끼리 선형종속이므로 0이 되고
pv는 qv에 대해 수직이므로 0이 된다.
= (1-2(qv · qv)) |pv|^2
또한 q는 단위 사원수이므로
qs^2 + qv · qv = 1이다.
1부분을 치환해보면
=qs^2 - qv · qv) |pv|^2
앞에서 정의한