행렬, 벡터, 선형변환에 대해 공부해봤다.
행렬과 벡터는 바꿔서 표현이 가능하고 선형변환해도 성질은 유지된다.
그렇다면 위치는 어떻게 표현해야할까?
벡터는 크기와 방향만 가지므로 정적인 위치를 표현하기에는 무리가 있다.
그래서 우리는 점,Point 을 쓴다.
어떠한 위치를 표현할 때 좌표로 그 해당 지점을 말한다.
우리가 점을 찍는다고 말할 수 있는 공간을 아핀 공간이라고 한다.
알아보자
아핀 공간이라는 말이 익숙치가 않다.
일반적으로 유클리드 공간은 아핀 공간이지만 벡터 공간이라고도 한다.
아핀 공간의 정의 자체가 벡터공간을 필요로하기 때문이다.
아핀 공간으로 벡터 공간을 형성할 수 있다고 알고 이해해보면 되겠다.
일반적으로 직교좌표계에서 점은 원점으로부터 각 축에 대해서 얼만큼 떨어져 있는가로 표현된다.
아래 그림처럼 표현된다.

이렇게 정의된 점이 아핀 공간에 있다고 했다.
도대체 아핀 공간이 뭘까??
++그냥 벡터공간이라고 알기 보다 더 정확히 정의해보자.
V라는 벡터 공간이 있을 때, 이 V 위에서 아핀 공간은 A라는 점들의 집합으로 정의된다.

V와 A 사이에는 위 2가지 두 대응이 존재한다고 한다.
또한 3가지 성질이 있다.


아 못알아듣겠네..
ㅎㅎ
첫 번째 대응부터 살펴보자.

점과 벡터공간을 X연산을 했더니 점이 나온다.
???
두 번째도 보자

** 여기선 첫 번째 대응의 X연산을 덧셈(+)이라고 생각한다.
이 때 (어떤 점과 벡터) 는 그 두 개를 +연산한 것과 일대일 대응관계를 이룬다는 말이다.
**일대일 대응이면 반대로도 가능 -> +연산은 다시 그 둘로 대응됨.
점과 벡터가 어떻게 + 연산이 되는거지???
근데 우리는 이미 알고 있었다.
++실제로 알고 있지만 일반화 해놓으면 모르는 경우가 많다.
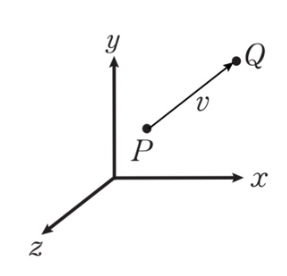
P(점) 에서 v(벡터)를 더해서 Q(점)이 나오는 것

이거 보면 무릎 탁 치겠다.
이미 알고 있는 것이다.
-> 그래서 아핀 공간에서 덧셈연산을 할 때는
벡터와 벡터의 연산인지, 점과 벡터의 연산인지에 유의해서 정확하게 말해야 한다.
2가지 대응에 대해 알아봤으니 3가지 조건(성질)을 다시 보자

1번 조건을 보자.
방금 했던 점과 벡터의 연산이다.
실제로 영벡터를 덧셈 연산해보면 첫 번째 조건이 만족함을 알 수 있다.
2번 조건을 보자
역시나 풀어서 연산해보면 성립한다.
3번 연산을 보자
유일한 벡터가 존재한다??
실제로 점 2개를 찍어보고 어떤 벡터가 만들 수 있을지 생각해보면 유일함을 알 수 있다.
반대로 Q에서 그 연산을 뺀다면 점 P가 나온다는 것도 알 수 있다.
**그래서 우리가 시작점에서 끝점을 빼는 연산이 그 벡터를 구하는 방법으로 배운 것이다. (고등학교에서)
벡터와 벡터의 연산 -> 벡터
벡터와 점의 연산 -> 점
점과 점의 뺄셈 연산 -> 벡터
위의 조건을 만족하는 공간이란 것이 아핀 공간이란다.
추상적으로 이해되겠지만 그래도 괜찮다. 넘어가자
점 다음은?
바로 선, Line이다.
하지만 2차원에서 선을 표현하는 것을 할 수 있지만
3차원에선 선을 표현하는 것이 불가능하다.
실제로 불가능하다기 보다는 ax + by + c = 0과 같이는 표현을 하지 못한다는 말이다.
++ 성분이 늘어나자너.. 때문에 사실 평면의 방정식이 되어버린다.
그래서 3차원에서는 매개변수 방정식(paramatic equation)을 통해 선을 표현한다.

어떠한 방향벡터와 점이 선을 표현할 수 있게 된다.
** 그 방향벡터는 점과 점을 뺀 벡터가 된다.
++ t는 음의 무한대~양의 무한대의 실수 범위를 가지고 있다.

이렇게 직선을 표현하는 과정에서
(1-t)와 t를 주목해보자
++이거 고등학교 때 기벡시간에 배운 거 같은데..?
점에다 스칼라 값을 곱하고 이를 더한다.
아핀 공간에서 점과 점의 덧셈은 안되는 줄 알았는데..?
하지만 벡터 공간의 선형조합처럼 아핀조합이라는 것이 있다.
선형 조합이 벡터들에게 임의의 스칼라 값을 곱해서 새로운 벡터를 만든다면
아핀 조합은 점들에게 특정 조건을 만족하는 스칼라 값을 곱해서 더하면 새로운 점이 나온다.
벡터는 임의의 스칼라고
점은 특정 스칼라 곱이야???
아핀 조합은 점과 벡터의 덧셈연산에서 나온다.
점에다 벡터를 더한다고 해보자.

쉽게 생각하기 위해서
P0가 중심이라고 생각하면
v1~ vn은 기저벡터라고 볼 수 있다.
즉, 기저벡터들은 다시 다르게 표현할 수 있다.
-> 점 - 점이 뭐라그랬지? 벡터라고 했다.

그럼.. 다시 v1 ~ vn 대신 위에 바꿔서 넣어보면..?

오...
뭔가 1-t 와 t 같아졌네??
위 식이 바로 새로운 점을 만드는 아핀 조합이다.
각 스칼라 값만 뽑아보자

** 특징이 보이는데 모든 점에 대해서 스칼라 값의 합이 1이됨을 알 수 있다.
이것이 바로 아핀 조합의 스칼라 조건이다.
기저벡터들의 조합으로 벡터공간이 형성되듯이
P0~ Pn의 점들 조합으로 아핀 공간이 생긴다.
와!! 신기하다.
아핀 조합에 참여한 점들은 임의의 점이 아니라
서로 아핀 독립(affinely independent)하다.
아핀 독립이란 쉽게 말해서 점 집합에서 임의의 한 점이 나머지 점들을 아무리 아핀 조합으로 한들 만들어질 수 없다는 것을 의미한다.
기저 벡터와 같이 이해하면 된다.
-> y벡터, z벡터를 아무리 조합해도 x벡터가 나오지 않는 것과 같다.
?? 근데 점들이 아핀 독립인지 내가 어떻게 구해????
이는 벡터를 이용해서 구한다.
정렬된 점들이 서로에게 아핀 독립이라면
이 점들을 차례대로 두 개씩 골라서 만들어지는 벡터 또한 선형 독립이 되는 것을 이용한다.
**차례대로 따라가야 기저벡터가 생긴다.
이 벡터들이 한 벡터 공간의 기저 벡터가 된다는 점을 이용하는 것이다.
때문에 P0를 중심으로하는 벡터 공간이라고 가정했던 것이다.
**아핀 독립인 점들의 집합을 단체,Simplex라고 하고 아핀 조합에 등장하는 스칼라 값들을 아핀 조합으로 생성되는 점의 무게중심좌표, barycentric coordinate 라고 한다.
다시 보자

즉, 이 매개변수 방정식은 아핀 조합임을 알 수 있다.
PQ벡터는 유일한 기저벡터가 된다.
이 아핀 조합은 1차원 아핀 공간을 생성하고 이것이 바로 선이 되는 것이다.
**면도 비슷하게 세 점을 아핀조합해서 2차원 아핀 공간을 생성한다.
직선이 아니라 선분을 표현하려면 어떻게해???
t값의 범위가 정해진 경우 선분이 되는 것이다.
예를 들어서
t가 0보다 크거나 같고 1보다 작거나 같은 범위를 가지면
P와 Q를 잇는 선분이 만들어질 것이다.
다음 시간에는 머리 아프지만 면에 대해서 알아보자
'Game Development, 게임개발 > 게임 수학,물리' 카테고리의 다른 글
| 아핀 공간, Affine Space - 3 [게임수학] (0) | 2021.04.01 |
|---|---|
| 아핀 공간, Affine Space - 2 [게임수학] (0) | 2021.03.31 |
| 쿼터니언(사원수), Quaternions (4) | 2021.03.31 |
| Linear Transformation, 선형변환들의 조합, 행렬곱 [게임수학] (0) | 2021.03.18 |
| 선형변환, Linear Transformation - 회전변환, 로드리게스 회전 공식 [게임수학] (0) | 2021.03.18 |