이제 정말 반도체에 대해 복잡해지는 단계에 왔다.
천천히 가보자
Thermal Motion
열운동 : 전계를 가하지 않았을 때에도 캐리어는 멈추어 있지 않고, 열에너지에
의하여 유한한 운동 에너지를 가지고 있다.
평균 운동 에너지(Average electron or hole kinetic energy) 는 당연하게 이렇게 구한다.


그렇게 구하고 속력은 이렇게 구한다


** Vth 는 Thermal velocity라고 하는데 반도체 내에서 가장 빠른 속력이라고 할 수 있다.
++ 고체 속에서는 충돌이 일어나기 때문이란 것만 알아두고 넘어가자.
++ 위의 식에서 T(온도)와 Vth(속력)의 관계 알고가자 ㅎㅎ
그러면 어떻게 움직일까??
전자와 정공은 열 속도로 움직이기는 하지만 단순히 직선 형태로 운동하지 않는다.
결정 내의 결함들과 산란(scattering)이 발생하여, 지그-재그로 움직임.

충돌 사이의 평균 자유 시간(mean free time) : ~ 0.1 ps
Net thermal velocity = 0 >> 열 운동은 전류를 생성시키지 않고, 열잡음(noise) 을 생성.
이제 Drift에 대해 알아보자
Drift : 전계(전기장)가 가해졌을 때 발생되는 캐리어들의 움직임.
전기장은 열 속도 위에 덧붙여진 드리프트 속도를 발생시킨다.

++ 전기장 방향은 (양전하 기준)
충돌 사이의 평균 자유 시간이 τmp이고, 매 충돌 때마다 전체 드리프트 운동량
mpv 을 잃어버린다고 가정하자.



충돌 사이에 얻는 드리프트 운동량은 힘과 평균 자유 시간의 곱과 같다.
위 식 오른쪽 2개는 외워야 한다.
** μp : hole mobility (cm2/V·s) , μn : electron mobility (cm2/V·s)
++ 뮤라고 읽는다
** Mobility(이동도) 가 클수록, 고속동작이 가능. (큰 전류)
전자 mobility가 더 큰데 그 이유는 전자 유효질량이 작기 때문이다.
예제를 하나 보고갈까? 여기엔 mean free path 도 나오는데 그냥 mean free time에서 나온 것이다.

다시 돌아와서 Carrier Scattering에 대해 알아보자
캐리어 산란에는 2가지가 있다.
1. Phonon Scatering (a.ka. Latice scatering)
2. (ionized)Impurity Scatering (a.ka. Coulombic scatering)
우선 phonon에 대해 먼저 알아보자면
Phonon scattering : 결정 내에 있는 원자의 진동을 입자로 나타낸 것을 포논이라 함.
결정 진동은 주기적인 결정 구조를 왜곡시키고, 따라서 전자 파동을 산란시킨다.

**포논 산란 이동도는 온도가 증가할 때, 감소한다. (산란이 강해진다.)
** 온도가 높아짐>> 원자 진동 증가 >> density 증가
** 충돌 증가>> mobility 감소
++참고로, 여기서의 phonon scattering은 좀더 정확하게 acoustic phonon scattering을 말함.
(optical phonon도 있는데 다음 번에 언급할거다.)
이번에는 Impurity scattering에 대해 알아보자
Ionized impurity scattering : 도펀트 이온은 반도체 결정 내의 고정된 전하이다.
다시 말해서, 쿨롱 힘을 통해서 전자와 정공이 운동 방향을 바꾸게끔 할 수 있다.
(운동 방향이 바뀐다는 것은 충돌같이 보이잖아?? 그래서 scattering)

**donor이온은 + acceptor이온은 - 가 되겠다.
높은 온도에서 더 빠른 열 속도를 가짐. 빠르게 지나쳐버리므로 이온에 의해 영향을 덜 받는다.
즉, 불순물 산란 이동도는 온도가 증가할 때, 증가한다. (산란이 약해진다.)
++ 너무 빠르니까 힘을 받는 시간이 짧다. 그러니까 운동방향을 바꿀만한 힘을 주지를 못한다는 얘기다.
++Na + Nd는 dophant 증가이다. 당연히 입자들이 많아지면 scattering도 많아지겠지?? 그래서 분모에 있다.
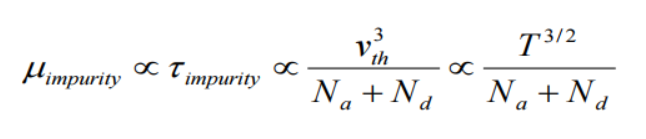
어차피 전체적인 것이 중요하니까 앞서 말한 2가지를 합쳐서 살펴보면??
Total scattering : scattering rate은 각각의 scattering rate을 더한 것이다.
따라서, 전체 mobility도 아래와 같이 된다.
**rate == 초당 몇번 // 이것을 구하려면 1번 충돌시간을 역수하면 되겠네?? mean free time 이용

저기 오른쪽 위의 식은 (Matthiessen rule) 이라고 부른다. 외워놓자.. 쉽잖아
x축은 도핑 농도를 뜻하는데
도핑 농도가 높아지면 당연히 impurity scattering이 커지고 mobility는 작아지겠지? 그렇다면 역수는 커져야한다.
그렇지만 그래프를 보면 끝에 saturation (포화)가 되어있다.
도핑농도가 아주 클 경우에는 “free-carrier screening” 때문에, 도핑 농도에 반비례하는 성질이 성립하지 않는다.
Free-carrier screening : 캐리어 농도가 커질 때, 캐리어들은 스스로 전체 에너지를 낮추는 방향으로 분포하게 되며, 도펀트 이온의 coulombic field 를 차폐한다. (너무 많으면 서로 상쇄한다고 보는 것이다)
그럼 이번엔 mobility의 온도 의존성을 살펴보겠다.
그림을 보기 전에 2가지를 알고 넘어가자
1. 도핑 농도가 낮을 때는, mobility는 phonon scattering(lattice scattering)에 의해 좌우된다.
2. 도핑 농도가 높을 때는, mobility는 impurity scattering에 의해 좌우된다.

우리는 이전에 식을 봐서 impurity와 phonon scattering이 서로 다른 온도의존성을 갖는 것을 안다.
그리고 내가 2가지를 알고 넘어가자고 했다.
오른쪽 위의 작은 그림을 보면 경향성이 나와있다.
결국 도핑농도에 따라서 둘 중 하나의 경향성을 따라가는 것이다.
그림 이해는 필수
그리고 우리는 속력을 구할 때 전기장의 세기와 속력은 비례한다고 배웠다.
그렇지만 속도에는 한계가 있다.
Velocity saturation이라고 한다.
앞에서의 속도와 전기장의 관계는 일반적으로 electric field가 작을 때에 성립한다.
Electric field 가 커지게 되면, 속도가 계속 증가하지 못하고 포화된다.
(앞서 말한 Vth, thermal velocity에 가까워진다)
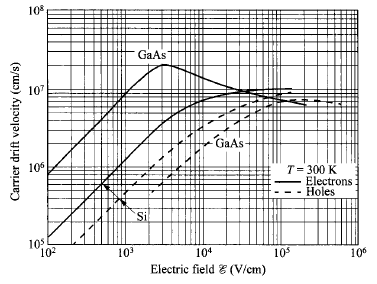
속도가 포화되는 이유는 운동에너지가 커지게 되면, 캐리어들과 강하게 상호작용을 하는 고 에너지의 포논(optical-phonon)을 생성하고, 운동에너지를 잃어버리게 되는 것이다.
++여기서 optical-phonon이다, 우리가 phonon scattering할 때 phonon 과는 다르다.
**우리가 쓰는 반도체들은 이미 속도포화영역에서 쓰고 있다. 왜냐면 반도체의 크기가 작아져서 그렇다.
또 속도가 포화되는 경우 말고 갑자기 빨라지는 경우도 있는데
Ballistic Transport 라고 한다.
탄도적 전송(ballistic transport) : device size가 평균자유행로(mean free path)보다 짧아지게 되면, scattering이 발생하지 않는 환경 속에서 캐리어가 움직임.
mean free path는 다시 말해서 충돌과 충돌 사이의 평균 거리이다.
즉, 반도체 소자가 작으면 충돌 안하고 움직일 확률이 높다는 것이다.
++Velocity saturation은 충돌 때문에 일어나는 것, 탄도적 전송은 충돌이 없어서 일어나는 것
Velocity overshoot : 속도 포화가 일어나지 못하고, 순간적으로 속도가 크게 증가 할 수 있게 됨.
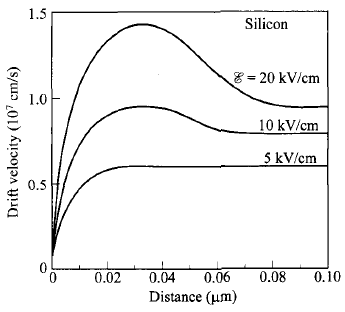
이 그림은 어디까지나 확률이다. 속도가 높아질 확률이 높은 것이지 device size가 작으면 무조건 저 속도를 가지는 것이 아니다.
'전자공학 > 반도체' 카테고리의 다른 글
| 반도체(9) Thermionic Emission, Tunneling, Space-Charge (0) | 2020.04.19 |
|---|---|
| 반도체(8) Drift,Diffusion, 드리프트 전류 , 확산 전류 (2) | 2020.04.19 |
| 반도체(6) Carrier in Semiconductor, 반도체의 전하 캐리어 (3) | 2020.04.18 |
| 반도체(5) Fermi-Dirac Distribution Function, 페르미 준위 (0) | 2020.04.18 |
| 반도체(4) DOS , Thermal equilibrium (열적평형) (0) | 2020.04.10 |