이제는 정말로 반도체와 직결되는 전류에 대해서 알아볼건데
드리프트와 확산에 의한 전류가 있따.
한 번 알아보자
우선 전류를 알아보기에 앞서서 참고해야할 사항이 있으니
가장 중요한 에너지 밴드 다이어그램과 전압, 전기장의 관계를 알아야한다.
관계를 알려면 전압과 전기장부터 알아야한다.
전압 : 단위 양전하당 전기적 위치 에너지의 차이. 양의 전압은 양 전하의 위치 에
너지를 증가시키고, 음 전하의 위치 에너지를 감소시킨다.
**에너지 밴드는 전자를 기준으로 그린 것이기 때문에 양의 전압은 에너지 밴드를 아래쪽으로 낮춘다.
전기장(electric field) 은 이렇게 구한다.
** 전압의 정의를 알아야 구할 수 있다는 말이다. ㅎㅎ

저 식을 해석하자면
Ec의 기울기, Ev의 기울기 Ei의 기울기, 에너지 밴드의 기울기 전기장은 비례한다는 것을 알아낼 수 있다.
그렇다면 전기장을 가했을 때 변할 다이어그램, 에너지 밴드 그림도 그릴 수 있어야 하지 않을까?
**그릴 수 있어야 한다. 필수로.



++여기서는 0.7V보다 0.7eV가 맞는 표현이다.
이제 Drift current에 대해서 알아보자

J = I/S로 표현하는데 I를 그렇다면 어떻게 구해야할까?
I = dq/dt다. 즉, 단위 시간당 전하량. 1초 동안 전하량을 구하려면..?
Unit area를 S라고 하자. 입자의 속도는 v 그렇다면 1초동안 V의 속력인 입자들이 S를 통과한 양은?
V*t*S*q*p (V 속력, t 시간, S 넓이, q 전하, p 개수) = I
그렇다면 J= I/S이니까 V*t*q*p (t=1)
The hole drift current density :

The electron drift current density :

The total drift current density :

++Conductivity(전도도) 와 Resistivity (비저항)


** hole의 이동방향 = 전류방향
** electron의 이동방향 = 전류 반대방향
++Resistance 와 Resitivity는 다르다.
그 다음은 도핑 농도와 비저항의 관계를 알아보겠다.
그림으로 알아보자

당연하게도
도핑농도가 높으면 캐리어 농도가 높은 것이고 당연히 비저항이 높아질 수 밖에 없다.
** Conductivity는 캐리어 농도, 이동도(mobility)에 좌우된다.
예제도 있다.


이제 확산에 대해서 알아볼 차례다.
확산이 뭔지부터 알고가자
확산(Diffusion) : 농도가 높은 곳에서 낮은 곳으로 이동하는 현상.
(캐리어 농도겠지?)

확산 전류(diffusion current) : 드리프트 전류에 추가하여, 반도체 내 두번째 전류 성분.
낮은 전도도의 경우와 불균일한 캐리어 농도 분포를 만들기 쉬운 경우에 중요한 전류 성분임.
**다시 말하자면 전도도가 높으면 Drift가 농도 기울기를 없애버리기 때문에 불균일 분포가 될 확률이 낮다.
그렇다면 확산 전류의 크기는 어떻게 구할까?
당연히 농도 차에 비례하겠지..?

++ 확산 상수(diffusion constant) : Dn , Dp
그림을 보고 잘 봐야하는 것이 농도가 높은 쪽에서 낮은 쪽으로 가는 거다???
확산에서 전자의 이동방향과 전류 방향을 잘 보고
정공의 이동방향과 전류 방향도 잘보자
그래서 저 (-)부호가 어디에 붙는지 잘 이해가 가야만한다!!
이동도와 확산계수는 밀접한 관계가 있는데,, 딱봐도
이동도가 높아야 확산 잘할 것 같이 생겼다. 그런데 이게 맞는 말이다.
그래서 이동도와 확산계수가 관련된
Einstein Relationship 을 설명할건데
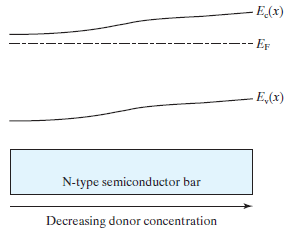
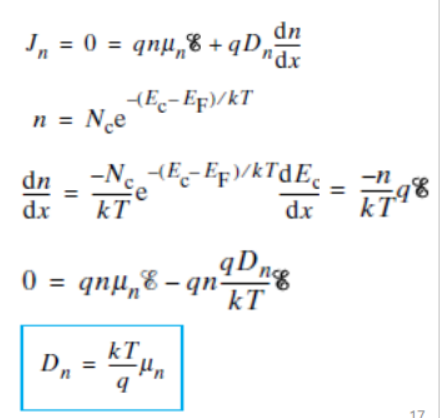
그림은 평형상태이다. (Thermal Equilibrium) 즉, 외부에서 에너지 인가가 없는 상태이다.
안정된 상태를 뜻하고 이는 전류 = 0 즉 Jn=0을 뜻한다.
저 식에서 dn/dx를 이용해 dn/dEc * dEc/dx를 이끌어낸다. 이는 x에 따라 Ec가 변하므로 그것을 이끌어내기 위함이다.
dEc/dx는 앞의 Electric Field 식 구할 때 봤다. (E(x) = 1/q * dEc/dx)
위의 유도를 통해 이동도와 확산 계수의 관계를 알아냈다.
예제를 또 보고가면

그렇다면 이제 확산, 드리프트 둘 다 배웠으니 종합하면?
Total Current, 전체 전류 : 반도체 내에 흐르는 전류는 일반적으로 드리프트와 확산 전류의 합으로 표현된다.


이런 식이 나온다.
저기에 Efp, Efn은 quasi-fermi라고 뒤에서 배운다.
미리 살짝 말하자면
Thermal equilibrium 은 전류가 0이고 그 때 n,p 구하는 공식은 위의 상황에서 쓸 수 없다
왜냐면 전류가 0이 아니니까(드리프트, 확산 전류)
그래서 quasi-equilibrium이라고 하고 그 때 n,p를 구할 때 Efp, Efn을 쓴다.
'전자공학 > 반도체' 카테고리의 다른 글
| 반도체(10) Recombination, Generation 전자 정공 재결합 및 생성 (4) | 2020.04.19 |
|---|---|
| 반도체(9) Thermionic Emission, Tunneling, Space-Charge (0) | 2020.04.19 |
| 반도체(7) Thermal,Drift,Scattering, 열운동,드리프트,충돌 (0) | 2020.04.19 |
| 반도체(6) Carrier in Semiconductor, 반도체의 전하 캐리어 (3) | 2020.04.18 |
| 반도체(5) Fermi-Dirac Distribution Function, 페르미 준위 (0) | 2020.04.18 |