컴퓨터 비전, CV 에서 대표적으로 사용되는 신경망이라고 알고 있다.
CNN 뉴스채널 아니고 합성곱 신경망이다. 이제 알아보자
이미지 분류하면 어떤 신경망을 쓰냐 하면
바로 CNN이 나올 정도로 이미지에 강한 면모를 보이고 있다.
++ Image Recognition=이미지인식
CNN을 이해하기 위해서는 합성곱(Convolution) 과 풀링(pooling)이란 개념을 알아야 한다.
사실 filter, stride, slide 등 많이 알아야 한다.
결국 어차피 이미지를 예를 들어 설명해볼 것이다.

이 그림을 보면 왜 컴퓨터가 이 사진을 차로 인식하게 되는가? 를 알려주는 순서다.
차를 넣으면 비트맵과 같이 매트릭스를 만들고 흑백일 경우 grayscale 0-255의 8비트를 가지며
filter로 슬라이딩하면서 특징맵(feature map)을 만들게 되고 다시 convolution layer에 넣어서 돌리고 pooling하고 최종적으로 나온 값을 하나의 array에 넣기 위해 flatten하게 되고
이는 결국 컴퓨터가 알아듣는 토대가 되는 것이다.
위에 모든게 다 나와있지만 아는 만큼 보인다고 나는 하나도 안보인다. ㅎㅎ
하나하나씩 알아보자
CNN은 내가 이미지와 관련된 컴퓨터 비전(computer vision)에 많이 쓰인다고 했다.
우선 이미지를 컴퓨터에게 입력시키기 위해서는
이미지는 우리의 감동의 대상이 아닌
그저 단순한 픽셀들이 모여서 만들어진 것이라고 봐야한다.
우리는 이것을 컴퓨터에게 전달해주어야 한다.
다시 말해서 2차원의 이미지를 전달해주어야 한다.
하지만 그렇다고 해서 요따구로 그냥 좌측 매트릭스를 입력하기 위해
단순하게 오른쪽처럼 Flatten을 해서 컴퓨터로 넘겨버리면 뭔지 알 수 있을까?
-> Flatten 층이란 3차원 행렬과 같이 다차원의 벡터를 1차원 벡터로 늘려파는 작업을 말한다.

즉, 왼쪽이 이미지라고 할 때, 컴퓨터가 그것이 이미지라고 받아들일까? 이미지의 특성도 알 수 있을까?
++뭐 진짜 단순한 경우에야 그렇지만.. 조금만 복잡해져도 불가능해질 것이다.
Dense Layer처럼 전결합층 하면
이미지 전체의 특징을 받아서 사용하는 것이 아니냐?
라고 할 수 있다.
하지만 실제로 이미지는 0번 픽셀부터 255번 픽셀까지 있다면0번과 관련이 깊은 픽셀은 1번이지 255번이 아니다.코와 관련된 것은 콧구멍이지 머리카락이 아니란 말이다.
만약 전 결합층으로 전달한다면
당장 아래와 같은 것만 해도 컴퓨터가 못알아들을 것이 뻔하다.
-> 정확하게 말해선 알아듣긴 하는데.. 비효율적이다.


그래서 나온 것이 CNN이다.
합성곱 신경망은 이미지를 컴퓨터가 잘 알아들을 수 있게 해준다.
적절한 필터를 활용하면 그것이 가능해진다.
합성곱층이란
현재 입력 이미지의 특정한 위치에서 이전 층에서 학습된 시각적 패턴의 특정한 조합이
탐지되었는지의 여부를 의미한다.
여기서 필터(filter)는 2 by 2 매트릭스로 되어있고 필터는 바로 특징을 찾는 것이라 말할 수 있다.
-> 위해서 말했듯이 인접 픽셀만을 골라내는 필터다.
이러한 필터로 해당 픽셀과 관계있는 픽셀을 특징으로하여 연산을 진행하게 된다.

이렇게 필터를 움직이는 과정에서 용어가 몇 가지 나오는데 알고가자.
영어설명은 이렇다.
Sliding filter is called stride.
Filter is feature identifier, sometimes called kernel,
and we call the area where filter stays a receptive field.
필터를 움직이는 것은 슬라이딩(sliding)
stride는 필터 위치를 옮기는 자체 (몇칸 이동)
필터는 kernel로도 불린다.
그리고 filter가 차지하고 있는 이미지의 공간을 receptive field라고 부른다.
근데 컴퓨터가 색도 알아듣나???
절대 아니다. 색을 숫자로 알려줘야 한다.
grayscale이라고 0-255의 범위를 가지고 명도를 나누어 놓아 구분하는 기준이 있다.
(255는 검은색 0은 하얀색)
그렇다면 위의 2는 어떻게 보일까??

요따구로 보이겠지???
filter 는 돌아다니면서 특징을 찾아다니는데 어떻게 특징일 것이라 생각하냐면 아래와 같은 연산을 한다.
(합성곱연산임) CNN

++filter에 해당하는 부분은 element를 대응하는 것끼리 곱한다.
**이 값이 클수록 특징을 가질 확률이 높은 것이고 작으면 확률이 낮은 것이다.
근데 위와 같이 합성곱 연산은 필터가 더 이상 슬라이딩 할 수 없을 때까지 반복하는데
그 결과 feature map(특징맵) 이 나오게 된다.
** filter size 또는 stride value에 따라 특징맵이 작아지게 된다.
-> 위 그림만 해도 2 by 2가 하나의 값으로 줄어들잖아?
4 픽셀 -> 1 개의 특징
다양한 이미지를 구분하기 위해선 그만큼 다양한 필터가 필요하겠지??
-> 즉, convolutional layer를 거치면서 특징들을 찾아내고 점점 high level의 특징들을 발견해나가는 것이다.
모든 특징을 찾게 되었다면 이제 실제로 예측할 수 있게 되는 것이고 과정이다.
근데 진짜 큰 이미지로는... 어떻게해?? 막 화소 높은거는??
그래서 pooling이란 개념이 생겼다.
실제로 유효하면서 주요한 특징을 추출하기 위해 사용하는 연산이다.
또한 특징맵의 크기를 줄이기도 한다.
** 사용하는 목적은 계산량의 감소다
조금 있어보이게 말하면
합성곱 연산에서 계산한 각 특징 맵을 다운샘플링, Downsampling 하는 것이다.
**필터와 비슷하다.


위에서 합성곱의 결과는 특징맵으로 나온다고 했다.
그래도 크네??? .. 그래서 풀링을 써보기로 했다.

위의 그림은 max pooling을 한 것으로
윈도우크기 2 by 2일 때 그 안에 있는 최댓값을 가져와서 특징맵을 줄이게 된다.
오른쪽과 같이 된 것이다. 그렇게 크기를 작게 함으로써 연산 시간을 줄인다는 것에 목적이 있다.
또한 overfitting(과적합)의 위험성을 낮춰주는 역할도 한다.
**다만 정보를 생략하는 것이기 때문에 정보를 잃는다는 생각도 가져야 한다.
**최근에는 풀링을 쓰지 않는다. 정보 손실이 크다고 생각했기 때문이다.
이전에는 계산량 감소로 인한 이득이 많았으나 기술의 발전으로 현재는 연산을 하는 것이 더 이득이 많아졌다.
하지만 필터링을 함으로써 입력보다 출력이 줄어드는 결과가 생기기도 하는데
그렇기에 zero padding이란 개념이 나왔다.
거의 모든 CNN에 적용되는 것이다.

convolutional layer를 거치면 항상 정보가 합성곱으로 인해서 줄어들게 되는데(특징맵이 줄어듬)
패딩을 적용하면 합성곱 연산은 수행되면서 특징맵의 크기가 입력한 데이터와 동일한 크기가 된다.
또한 zero padding이라는 것은 0으로 겉을 둘러싼다는 말이기에 입력데이터의 경계역할도 한다.
(이미지가 어디까지인지 구분이 가능하다는 얘기)
만약 grayscale이 아니라면...?

이렇게 RGB도 CNN을 적용하기 위해 이렇게 바꿀 수 있다.
다른 색도 HSV, CMYK 마찬가지다.
결국 이렇게 복잡하고 크기가 커질수록 CNN을 써야한다.
The role of the ConvNet is to reduce the images into a form which is easier to process, without losing features which are critical for getting a good prediction.
위의 말 같이 CNN이 이미지의 연산을 줄이면서 특징을 뽑아내니까!!
그렇게 해서 맨 앞에 나온 것처럼 총 정리해보자면??
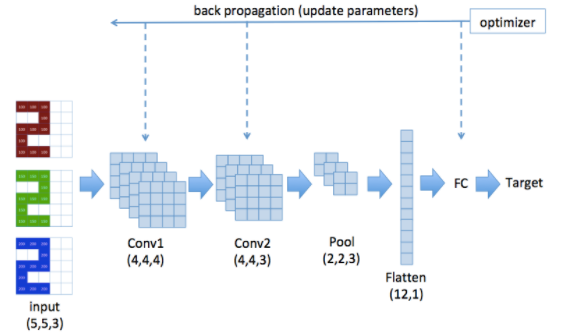
Conv1 에는 4개의 필터가 있어서 4개의 레이어가 나온다.
Conv2에는 3개의 필터가 있어서 3개의 레이어가 나온다
Pooling Layer에서는 stride size가 2이기 때문에 2 by 2 매트릭스의 특징맵을 얻게 된다.
또한 (2*2)*3 =12 결국 12개의 값이 있기 때문에 Flatten할 때 12의 크기를 갖게 된다.
그 Flatten 한 것을 Fully Connected Layer에 입력으로 넣어준다.
Output은 결국 Prediction이 나올 것이다.
CNN은 지도 학습이기 때문에 Target 값을 주면서 역전파를 통해 loss를 줄여가는 값을 갖는 parameter 조정을 하게 된다.

참고 링크
github.com/minsuk-heo/deeplearning/blob/master/src/CNN_Tensorflow.ipynb
'데이터 사이언스(Data Science) > 딥러닝, Deep Learning, 심층학습' 카테고리의 다른 글
| 신경망 기본 원리 - 합성함수 (2) | 2021.09.10 |
|---|---|
| LSTM, Long Shor Term Memory ; RNN 확장 신경망 (0) | 2021.01.13 |
| RNN, Recurrent Neural Network; 순환 신경망이란? (0) | 2021.01.07 |
| [DL] 퍼셉트론(Perceptron) (0) | 2020.08.20 |