RNN은 이미 배웠다.
어텐션이 RNN의 단점을 보완하기 위해 나온 것처럼
LSTM도 그 RNN을 보완하기 위한 방법이다.

특히 길이가 길어질수록 앞쪽의 데이터의 내용이 뒤로 전달되지 않는 장기 의존성 (Long-Term Dependency)가 발생하기에 LSTM으로 이를 해결하고자 했다.
Hence standard RNNs fail to learn in the presence of time lags greater than 5 – 10 discrete time steps between relevant input events and target signals.
The vanishing error problem casts doubt on whether standard RNNs can indeed exhibit significant practical advantages over time window-based feedforward networks.
The Long Short Term Memory architecture was motivated by an analysis of error flow in existing RNNs which found that long time lags were inaccessible to existing architectures, because backpropagated error either blows up or decays exponentially.
LSTM은 기본적으로 RNN의 HS를 계산하는 방식이 조금 다르다.
그리고 HS 외의 셀 상태값이라는 것을 추가시켰다.
도식화된 모습을 보자면 이렇다.

RNN과 비슷해보이지만 내부가 조금 다르게 생겼다.
LSTM은 HIdden Layer에 입력 게이트, 삭제 게이트, 출력 게이트를 추가해서 불필요한 것은 지우고 필요한 것을 정하는 작업을 하게 했다.
++바로 그 값이 메모리 상태 값(cell state)이라고 보면 되겠다.
LSTM이 Hidden State + Cell State 을 연산하는 것이라고 보면 되겠다.

근데 셀 상태도 보니까 이전의 셀 상태 값을 현 시점의 입력으로 사용되는 것을 볼 수 있다.
HS = Hidden State, CS = Cell State
결국 HS, CS를 우리는 둘다 구해야한다.
** 셀 상태를 장기상태라 부르고 은닉 상태를 단기 상태라 부르기도 한다.
그래서 위에 3개의 게이트를 추가시켰기에 이를 통해서 값을 구하려고 한다.
**각 게이트에는 시그모이드 함수가 존재해서 (0~1)의 값으로 게이트를 조절함.
-
입력 게이트의 역할

수식과 함께 보면 메스꺼울까?

수식이 나왔다.
입력게이트의 역할은 현재 정보를 기억하는 것이다.
"""
현재시점 t의 x 값과 입력게이트로 이어지는 가중치 Wxi 곱한 값 +
t-1 시점의 HS값과 입력게이트로 이어지는 가중치 Whi 곱한 값
**b 는 bias (편향)값이겠지
을 시그모이드 함수에 넣으면
t시점의 i 값이 된다.
"""
gt도 어떻게 나오는지 알겠지??
결국 i 값은 (0~1)의 범위를 g 값은 (-1~1)의 범위를 [하이퍼볼릭함수라서]
가지게 되는데 이 2개의 값으로
이번 정보를 얼마나 기억할 지 정하는 것이다.
-
삭제게이트의 역할

얘도 어떤 식으로 계산되는 지 알겠지??
얘는 값이 하나지??
이 값이 삭제 과정을 거쳐서 나온 정보의 양이라고 볼 수 있다 (0 ~ 1)의 범위
0에 가까우면 거의 남아있는 정보도 0 -> 삭제가 많이 되었다.
-
CS를 구하는 방법이다.
*왜 출력게이트 안구하고 먼저 나왔느냐???
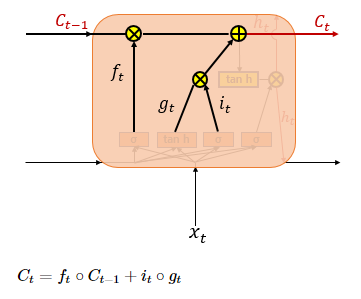
Ct의 입력이 f, i, g인데 앞에서 다 구했잖아?? ㅎ
즉, 입력게이트, 삭제게이트를 지나온 것들이다.
입력 게이트에서 구한 값들을 원소별 곱을 해준다. (entrywise product)
-> 크기가 같은 두 행렬끼리만 가능 (이 값들이 이번에 선택되어 기억할 값임)
입력게이트에서 삭제게이트의 결과값과 더한다.
그 값이 결국 현재 시점 t의 Cell State가 된다.

아까 f의 값의 범위가 0~1이라고 했고 0이라면 다 삭제되었다고 했지?
만약 f의 값이 0이된다면 이전 Cell State의 값이 몇이든 삭제게이트의 결과값이 0이 된다.
그렇게 되면 입력게이트의 값만 Cell State에 영향을 줄 수 있다.
-> 입력게이트는 현재 시점의 입력임
다시 말해서 이전 시점의 입력을 얼마나 반영할까? 는 삭제게이트가 정하고
현재 시점의 입력은 얼마나 반영할까? 는 입력게이트가 정하는 것이다.
-
출력게이트와 HS

마지막으로 HS를 구하기 위해 출력게이트를 이용하면 되겠다.
출력게이트 역시 식을 보면 알 수 있다.
o값을 구하는게 i랑 비슷하네??? -> 맞다. 비슷하다
o값이 바로 HS로 쓰이는 것이아닌 하이퍼볼릭탄젠트 함수를 적용해준다. (-1 ~ 1) 값의 범위를 가짐
때문에 해당 값은 출력게이트 값과 연산되면서 현재 시점 t의 은닉 상태를 결정하는데 쓰인다.
이 HS 값은 출력층으로도 나간다.
(ht가 2군데로 나누어짐)
결국 이런 식으로 계산이 되어 이전 시점의 정보를 얼마나 남길지 정해서
길이가 길어짐에도 정보가 남아있게 하는 것이다.
이후 LSTM은 Bi-LSTM으로 발전해서
양방향으로도 가능하게 되었다.
참고
machinelearningmastery.com/gentle-introduction-long-short-term-memory-networks-experts/
'데이터 사이언스(Data Science) > 딥러닝, Deep Learning, 심층학습' 카테고리의 다른 글
| CNN, Covolutional Neural Network, 합성곱 신경망이란? (0) | 2021.09.23 |
|---|---|
| 신경망 기본 원리 - 합성함수 (2) | 2021.09.10 |
| RNN, Recurrent Neural Network; 순환 신경망이란? (0) | 2021.01.07 |
| [DL] 퍼셉트론(Perceptron) (0) | 2020.08.20 |