우선 도핑을 설명하기 전에
전도 전자와 정공을 다시 짚고 넘어가자

이 모든 설명의 큰 흐름은 에너지는 안정된 상태로 가려는 경향이 있다로 설명한다.
전도 전자의 에너지 중, Ec보다 큰 모든에너지는 전자의 운동에너지에 해당한다.
에너지의 기준을 어떤것으로 잡느냐에 따라 달라지는 것이다.
전자와 정공은 전기장 내에서 가속됨으로써 에너지를 얻을 수 있고, 결정 내에서 충돌로 인해 에너지를
잃을 수 도 있다.
전압의 정의: "양전하" 기준의 전기적 위치에너지 차이!!
즉 전압을 걸면 band가 내려가는 모양이 나온다. // 에너지 밴드 다이어그램에서 전자는 밑으로 가려고하고 정공은 위로

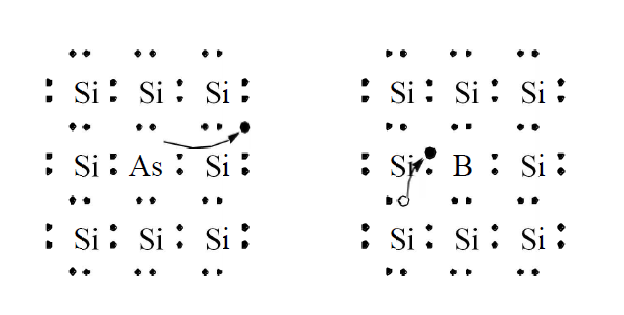
도핑 이라는 것을 설명하기 전에 알고가자
진성반도체(Intrinsic semiconductor) 라는 것은 도핑이 안 된 반도체를 말한다.
열에너지에 의해서만 electron hole 쌍이 형성된다고 보면 된다.
그렇지만 우리는 전도성을 높여야할 때가 있다. 그래서 도핑이라는 방법을 생각해냈다.
도핑은 의도적으로 캐리어의 농도를 높이는 것으로
N-type, P-type 도핑 2가지가 있다.
각각 Donor, Acceptor로 불리고 전자농도, 정공농도를 증가시키는 것이다.
도핑을 했다고 해서 전체적으로 +,- 전하를 띄는 것은 아니다. 중성원자를 집어넣은 것이다.

이온화 에너지(ionization enerygy) : 도핑된 불순물이 실제로 전자나 홀을 형성하는데 필요한 에너지
약 50meV로 매우 작아서 상온에서는 전부다 이온화 된다고 본다.
** 왜 이온화냐고??
Donor가 전자가 5개였는데 전도전자가 만들어지면 Donor 자신은 양이온이 된다는 뜻이다
즉 캐리어 농도 = 도핑한 불순물 농도
이제 실효질량에 대해 알아볼 것인데 왜 필요하냐? 설명해보자
우선 결정 내의 전자에 대한 파동함수는 3차원 슈뢰딩거 파동방정식을 풀어서 얻을 수 있다.
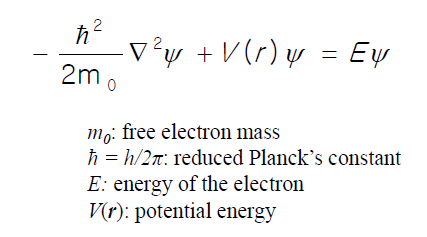

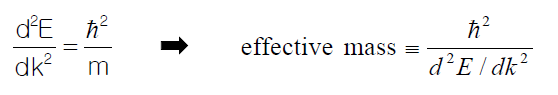
그렇다고 하니까 우리는 받아들이면 된다. 증명을 해줬으니 우린 증명 시도는 할 수 있으나 성공까진 안바란다.
해는 exp(±k·r) 형태가 되며, k는 파동 벡터(wave vector)이고, “ 2π/전자의 파장”이며 E의 함수이다.
결정 내의 전자의 움직임은 자유 공간과는 다른데 다시 말해서 결정 내의 주기적인 potential의 영향을 받는다
만약 외부에서 힘(전기장, 확산)을 가하게 되면 결정 내 전자 운동방정식은 이렇게 될텐데

ext = external(외부) int = internal(내부) = 주기적인 potential
내부힘을 항상 고려하는 것을 비효율적이다.
왜냐면 항상 우리는 대부분 외부에서 힘을 걸었을 때의 전자의 움직임을 살피니까.
그래서 나온 것이 유효질량이다
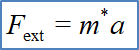
내부의 potential이 고려된 질량으로써, 이를 이용하면 기존의 물리법칙 이용시 외부의 힘만 고려하면 된다.
'전자공학 > 반도체' 카테고리의 다른 글
| 반도체(6) Carrier in Semiconductor, 반도체의 전하 캐리어 (3) | 2020.04.18 |
|---|---|
| 반도체(5) Fermi-Dirac Distribution Function, 페르미 준위 (0) | 2020.04.18 |
| 반도체(4) DOS , Thermal equilibrium (열적평형) (0) | 2020.04.10 |
| 반도체(2) 에너지 밴드 모델 (Energy band model) (0) | 2020.04.10 |
| 반도체(1) Si (실리콘) 과 전자 정공 (0) | 2020.04.10 |