노는 게 제일 좋아

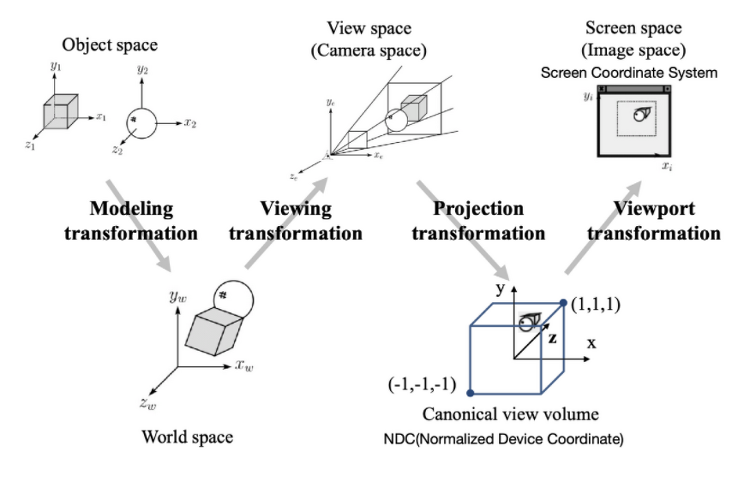
**21.11.11 업데이트 **21.12.22 업데이트 게임의 오브젝트가 우리 스크린 위에서 실제로 움직이기까지 정말 많은 과정을 거친다. 그 과정들은 Transformation이고 특히 좌표 변환이 엄청나게 이루어진다. -> 행렬의 계산은 은근히 연산이 많기에 이를 해결한다면 렌더링에 도움이 될 것 같다. 알아보자 우선 요약하자면 Local World (Model Space) World (Model Space) View (Camera Space) View (Camera Space) 정규 뷰 볼륨, Canonical view volume (Proejection) Canonical view volume Screen 순서대로 알아보자 3D 모델의 폴리곤 메시가 가진 모델 공간의 Local 좌표에서 Worl..

//21.12.22 업데이트 좌표계도 많은데 동차 좌표계라는 새로운 것이 튀어나왔다. 무엇인지 알아보자 사실 근본적인 정의보다 우리가 어떻게 이해해야하고 왜 이렇게 사용하는지를 중점에 두고 알아보자 3차원의 좌표는 (x,y,z) 3가지 성분으로 표현된다. 하지만 동차좌표에서는 여기에 무한원점이라는 개념을 추가시킨다. -> 무한원점의 개념이 어려우면 아래와 같이 이해하자 -> 사실 4차원의 성분이 0이면 벡터, 1이면 점이라고 설명하는 경우도 많다.(대부분) (이 말은 3개의 성분가지고는 벡터인지 점인지 알 수 없지만 4번째 차원의 정보로 구분하겠다는 말이다.) ??? 근데 굳이 벡터인지 점인지 구분해야하나???? 이는 방향파악과 변환에 중요하기 때문인데..? ** 방향과 이동변환, 투영변환을 용이하게 하..

물론 내가 선형대수학을 공부할 때 회전변환을 공부하였다. [Game Developer, 게임개발자/게임 수학,물리] - 선형변환, Linear Transformation - 회전변환, 로드리게스 회전 공식 [게임수학] [Game Developer, 게임개발자/게임 수학,물리] - 선형변환, Linear Transformation - 회전변환, 로드리게스 회전 공식 [게임수학] 하지만 렌더링에서 좌표자체를 회전변환시켜 구현한다는 것이 아니라 다른 방법을 알아보고자 한다. 알아보자 분명 회전변환 식이 이렇다. 세타만큼 회전하고 싶다면 해당 좌표를 넣어 값을 얻으면 될 것이다. 하지만 변환된 좌표를 얻으려면 2차원의 경우 곱셈 2번과 합연산 1번을 2번을 해야 각각 변환된 x' , y' 이 나올 것이다. 픽셀..

3D 게임에서는 플레이어의 몰입을 위해 물체들을 실사와 같게 만드려고 노력한다. 그 중 빛에 대해서 실제와 같이 표현하려고 한다. 빛은 게임 속에서 어떻게 구현할 수 있을까??? 우리는 광원이 있다면 해당 광원에 대해서 물체의 어느 부분의 밝기를 올려야 하는가? 라는 질문을 하게 된다. 구가 있다고 해보자. 광원이 어디있다고 생각하는가? 아마 바로 머리위에서 조금 왼쪽에 있다고 생각할 것이다. 왜 이 그림을 보자마자 그렇게 느꼈나? 저것도 실제가 아닌 그림일 뿐인데..? 그 이유는 정말 실제와 같이 생겼기 때문이다. 구의 좌표를 알고 광원에 대한 방향벡터를 알 수 있다면 해당 지점에서의 밝기를 결정할 수 있겠다. 우선 정사영이란 것을 배웠다면 이해하기는 쉬워진다. 정사영은 직선으로 빛이 내리쬐고 물체에는..

게임을 들어가보면 항상 설정이 있는데 그래픽부분에 가보면 안티앨리어싱 켜키,끄기라는 탭이 거의 있다. 나는 특히 콜오브듀티를 할 때 많이 봤는데 내가 게임에 대해서 공부하지 않았을 때에는 그것이 그냥 선을 부드럽게 해주는 기능이라고 알고 있었다. 하지만 틀린 설명은 아니지만 왜 처음부터 부드럽게 나오지 않으며 어떻게 부드럽게 만드는 지에 대해서는 알지 못했다. 그래서 더 자세히 알아보았다. 우선 왜 만들어지느냐? 어떠한 것을 렌더링 할 때 알고리즘의 특성상 생기는 바람직하지 않은 아티팩트(Artifact) 중에서 특히 성가신 "재기, jaggies" 라는 형태가 나오는데 이 재기는 컴퓨터 디스플레이의 특성으로 도트를 모아 이미지를 구현하기 때문에 생긴다. 화면 해상도를 올려서 재기를 줄일 수 있지만 해상..

물론 게임 엔진 자체에서.. 충돌판정을 하는 툴을 제공하나 그런 것도 좋지만 원리 자체를 이해해보자. 당연하게 생각하는 것에 의문을 품으면 발전할 수 있다. **꼭 그런 것은 아니다. 충돌은 2가지로 판단한다. 1. 그냥 충돌했다. 2. 충돌하지 않는 경우를 제외하면 충돌했다. 2가지 접근 방식으로 알아볼 것이다. 우선 가장 간단한 것은 사각형(2D) 간의 충돌 판정이다. 왜 간단하냐면.. 사각형은.. 가로, 세로 길이만 알면 바로 좌표를 정할 수 있어서 그렇다. 물론.. 우리는 직사각형과 같은 것이 제일 좋다. 충돌도.. 이렇게 하면 조금 귀찮아진다. ㅎ 우선 충돌이 일어난다는 것은 자신의 영역에 다른 무엇인가가 들어왔다는 것이다. 아래와 같은 영역을 생각해보자 Ractangle 1 0

게임의 몰입을 위해서 우리는 별 짓을 게임에 다한다. 그 중 하나가 원근감이다. 원근감이 없다면 현실처럼 느껴지지 않으며 몰입하기 힘들다. 때문에 게임에서 원근감을 표현하는 것은 중요하다. **모든 종류의 게임에서 그런 것은 아니다. 우리는 미술시간에 소실법이라고 배웠다. 게임은 미술시간에 배운 것도 사용한다. 실제로 3D 게임에서는 '시추대' 라는 개념을 사용한다. 이러한 용어가 중요한 것은 아니고 그냥 시추대는 플레이어가 바라보는 시점을 기준으로 하고 디스플레이의 면을 바닥 면으로 하는 사각뿔을 디스플레이 너머까지 연장하는 것이다. 음.. 아래와 같은 느낌 ** Perspective 에서가 그렇다. Orthogonal은 그냥 그대로 투영한 것이다. 즉, 위와 같이 한다면 디스플레이 상에서 물체를 표현..

수면마취가 되어서 어디론가 이동한 후 깨어 창 밖을 바라보니 산이 뒤로 이동하고 있다. 과연 그럴까? 즉, 우리는 관찰만으로는 내가 운동하는지 내가 관측하는 물체가 운동하는지 알 수 없다. 그래서 말하려는 것이 무엇이냐? 배경을 움직여보기로 했다. 배경을 맵칩이 아니라 한 장을 밀면서 표현하는 방법은 2D게임에 정말 많이 쓰인다. 즉, 유저가 보는 카메라가 배경에 따라 움직이거나 배경이 카메라를 기준으로 움직여야 한다는 것을 말한다. 카메라를 고정하든.. 배경을 고정하든 맘대로 하자. (현실에서는 배경이 고정된 것을 참고) 배경도 물체랑 비슷하게 움직이게 하면 된다. bg.x = VIEW_WIDTH / 2.0f - camera.x; 위와 같이 배경이미지의 좌표를 카메라를 이동시켜 구해도 되고 그 반대도 ..

현실의 운동과 컴퓨터가 계산한 운동이 정확히 같을까? 디지털이 아날로그와 정확히 같을까? 아날로그는 모든 것을 표현할 수 있지만 디지털에는 표현할 수 없는 것이 있다고 흔히 말한다. 아날로그 시계는 이 세상에 존재하는 모든 '시각'을 가리킬 수 있다. 예를 들어 해시계는 연속적이다. 반면 디지털시계는?? 아무리 정확한 시계라도 불연속이다. 서론이 길었다. 즉, 우리는 물체의 운동을 컴퓨터에 구현하는데.. 힘이 많이 든다. 문과로 넘어가게 된 계기들 중 하나인 뉴턴의 첫번째 방정식을 가져와보자 F = ma Equation of motion이다. 운동방정식인데 이것 때문에 여럿 보냈다. 즉, a = F/m으로 다시 표현될 수 있다. 우리는 위치 - > 속도 - > 가속도를 구할 수 있다. 바로 시간에 대해 ..

이전의 글에서는 기저벡터의 이동으로 표현할 수 있는 운동은 다 구현이 가능하다고 했다. 원운동도 그에 해당하느냐? 물론 해당한다. 이전의 글에서 라디안으로 모든 방향을 기저벡터로 나눌 수 있었고 구현이 가능했다. [Game Developer, 게임개발자/게임 수학,물리] - 게임 물리 - 라디안의 이용 그러니까 원운동도 가능하다고 생각하는게 당연하다. 원운동이란 구심력 때문에 생기는 운동이라고 보면 된다. 하지만 새로운 개념이 나오는데 원운동의 상태를 표현할 때는 '각속도' 라는 것이 나온다. 속도라는 것이 시간당 가는 거리라고 본다면 각속도라는 것은 시간당 진행한 각도라고 볼 수 있다. 등속 원운동에서는 모든 곳에서 각속도가 같을 것이다. 그래서 2 Pi를 주기 T로 나누는 것으로 각속도를 구하기도 한..